题目内容
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )

A. 2B. 2.2C. 2.4D. 2.5
【答案】C
【解析】
根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
连接AP,
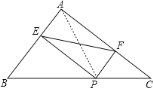
∵在△ABC中,AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
即∠BAC=90°,
又∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF=AP,
∵AP的最小值即为直角三角形ABC斜边上的高,即2.4,
∴EF的最小值为2.4,
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小莉和她爸爸两人沿长江边扬子江步道匀速跑步,他们从渡江胜利纪念馆同时出发,终点是绿博园.已知小莉比她爸爸每步少跑![]() ,两人的运动手环记录时间和步数如下:
,两人的运动手环记录时间和步数如下:
出发 | 途中 | 结束 | |
时间 |
|
|
|
小莉的步数 | 1308 | 3183 | 8808 |
出发 | 途中 | 结束 | |
时间 |
|
|
|
爸爸的步数 | 2168 | 4168 |
|
(1)表格中![]() 表示的结束时间为 ,
表示的结束时间为 ,![]() ;
;
(2)小莉和她爸爸两人每步分别跑多少米?
(3)渡江胜利纪念馆到绿博园的路程是多少米?