题目内容
如图,PA为⊙O直径,过弧AC的中点H作PC的垂线交PC的延长线于点B,若HB=6cm,BC=4cm,求⊙O直径.
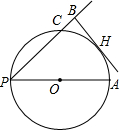

连接AC,OH,交于点G,
∵AP为直径,
∴∠ACP=90°,
∵HB⊥PB,
∴∠PBH=90°,
∴∠ACP=∠PBH,
∴AC∥BH,
∵H为
的中点,
∴OH⊥AC,G为AC的中点,
∴BH⊥OH,即BH为圆的切线,
∴四边形BCGH为矩形,
∴BC=GH=4cm,CG=BH=6cm,
∵OG为△ACP的中位线,
∴OG=
PC,
设圆的半径为xcm,则OH=xcm,PA=2xcm,
OG=OH-GH=(x-4)cm,PC=(2x-8)cm,AC=2CG=12cm,
在Rt△ACP中,根据勾股定理得:PA2=AC2+PC2,
即(2x)2=122+(2x-8)2,
解得:x=6.5.
则圆的直径为13cm.

∵AP为直径,
∴∠ACP=90°,
∵HB⊥PB,
∴∠PBH=90°,
∴∠ACP=∠PBH,
∴AC∥BH,
∵H为
 |
| AC |
∴OH⊥AC,G为AC的中点,
∴BH⊥OH,即BH为圆的切线,
∴四边形BCGH为矩形,
∴BC=GH=4cm,CG=BH=6cm,
∵OG为△ACP的中位线,
∴OG=
| 1 |
| 2 |
设圆的半径为xcm,则OH=xcm,PA=2xcm,
OG=OH-GH=(x-4)cm,PC=(2x-8)cm,AC=2CG=12cm,
在Rt△ACP中,根据勾股定理得:PA2=AC2+PC2,
即(2x)2=122+(2x-8)2,
解得:x=6.5.
则圆的直径为13cm.


练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 .
.