Question

【题目】乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车出发2h后休息，与甲车相遇后，继续行驶．设甲、乙两车与B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：
（1）乙车休息了h．
（2）求乙车与甲车相遇后y乙关于x的函数表达式，并写出自变量x的取值范围．
（3）当两车相距40km时，求x的值．

Answer 1

【答案】
（1）0.5
（2）解：设乙车与甲车相遇后y乙关于x的函数表达式为：y乙=k1x+b1，

y乙=k1x+b1图象过点（2.5，200），（5，400），

得 ，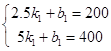

解得 ，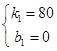

乙车与甲车相遇后y乙与x的函数解析式y乙=80x；

（3）解：设乙车与甲车相遇前y乙与x的函数解析式y乙=kx，图象过点（2，200），

解得k=100，

∴乙车与甲车相遇前y乙与x的函数解析式y乙=100x，

0≤x＜2.5，y甲减y乙等于40千米，

即400﹣80x﹣100x=40，解得 x=2；

2.5≤x≤5时，y乙减y甲等于40千米，

即2.5≤x≤5时，80x﹣（﹣80x+400）=40，解得x= ，

综上所述：x=2或x= ．

【解析】解：（1）设甲车与B地的距离y（km）与行驶时间x（h）之间的函数关系式为y=kx+b，

可得： ，

解得： ．

所以函数解析式为：y=﹣80x+400；

把y=200代入y=﹣80x+400中，可得：200=﹣80x+400，

解得：x=2.5，

所以乙车休息的时间为：2.5﹣2=0.5小时；

所以答案是：0.5；