题目内容
如图，D是线段AC的中点，E是线段AB的中点．已知AD=2.5，BC=2．求线段AB和EC的长度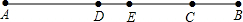
分析：解答此题的关键是明确各线段之间的关系，然后根据已知条件即可求出线段AB和EC的长度．
解答：解：∵D是线段AC的中点，
∴AC=2AD=2×2.5=5，
∵BC=2，
∴AB=AC+BC=5+2=7；
∵E是线段AB的中点，
∴BE=
AB=
×7=3.5，
∴EC=BE-EC=3.5-2=1.5．
答：线段AB的长度是7；EC的长度是1.5．
∴AC=2AD=2×2.5=5，
∵BC=2，
∴AB=AC+BC=5+2=7；
∵E是线段AB的中点，
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴EC=BE-EC=3.5-2=1.5．
答：线段AB的长度是7；EC的长度是1.5．
点评：此题主要考查学生对两点间距离的理解和掌握，此题难度不大，属于基础题．
练习册系列答案
相关题目
2、如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线L上取一点P，使∠APB=30°，则满足条件的点P的个数是（ ）
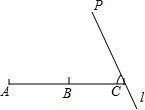如图，B是线段AC的中点，过点C的直线l与AC成50°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是（ ）| A、1个 | B、2个 | C、3个 | D、无数个 |
如图，M是线段AC的中点，N是线段CB的中点．
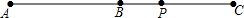如图，B是线段AC的中点，P是BC上一点，若PA=a，PC=b，则线段PB的长是（ ）| A、a-b | ||
B、
| ||
| C、2a-3b | ||
D、
|