题目内容
2、如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线L上取一点P，使∠APB=30°，则满足条件的点P的个数是（ ）分析：过点B作BP⊥AC，交直线l与点P，连接PA，由△PBC≌△PBA，从而可求得∠APB=∠CPB=90°-∠PCB=30°．
解答：
解：过点B作BP⊥AC，交直线l与点P，连接PA
∵AB=BC，PB=BP，BP⊥AC
∴△PBC≌△PBA
∴∠APB=∠CPB=90°-∠PCB=30°
以上图中的AP为直径作圆，直线l与该圆是相交的关系，另一个交点也满足条件．
所以满足条件的点P的个数为2个．
故选B．
解：过点B作BP⊥AC，交直线l与点P，连接PA∵AB=BC，PB=BP，BP⊥AC
∴△PBC≌△PBA
∴∠APB=∠CPB=90°-∠PCB=30°
以上图中的AP为直径作圆，直线l与该圆是相交的关系，另一个交点也满足条件．
所以满足条件的点P的个数为2个．
故选B．
点评：本题利用了等腰三角形的性质和全等三角形的判定和性质．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
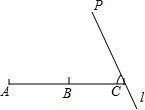如图，B是线段AC的中点，过点C的直线l与AC成50°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是（ ）| A、1个 | B、2个 | C、3个 | D、无数个 |
如图，M是线段AC的中点，N是线段CB的中点．
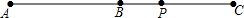如图，B是线段AC的中点，P是BC上一点，若PA=a，PC=b，则线段PB的长是（ ）| A、a-b | ||
B、
| ||
| C、2a-3b | ||
D、
|