题目内容
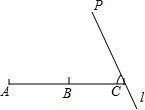如图，B是线段AC的中点，过点C的直线l与AC成50°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是（ ）| A、1个 | B、2个 | C、3个 | D、无数个 |
分析：若以AB为边作等边三角形，以等边三角形另一顶点为圆心，以等边三角形边长为半径作圆，圆心角∠AOB=60°．圆与l交于两点，根据圆周角定理可知：这两点都符合题意的要求，由此得解．
解答：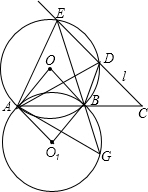
解：如图所示，
以AB为边作等边三角形，
设等边三角形的另一顶点为O和O1，
以点O和点O1为圆心，以AB为半径作圆，圆O与直线L交于D、E两点，圆O1与直线L无交点，
则有∠AEB=∠ADB=
∠O=30°，
∠AGB=
∠AO1B=
×60°=30°．
因此满足条件的点有两个：E、D．
故选B．
解：如图所示，以AB为边作等边三角形，
设等边三角形的另一顶点为O和O1，
以点O和点O1为圆心，以AB为半径作圆，圆O与直线L交于D、E两点，圆O1与直线L无交点，
则有∠AEB=∠ADB=
| 1 |
| 2 |
∠AGB=
| 1 |
| 2 |
| 1 |
| 2 |
因此满足条件的点有两个：E、D．
故选B．
点评：本题主要利用了圆周角定理和等边三角形的性质进行解答．作出辅助圆和辅助三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
2、如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线L上取一点P，使∠APB=30°，则满足条件的点P的个数是（ ）
如图，M是线段AC的中点，N是线段CB的中点．
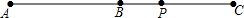如图，B是线段AC的中点，P是BC上一点，若PA=a，PC=b，则线段PB的长是（ ）| A、a-b | ||
B、
| ||
| C、2a-3b | ||
D、
|