题目内容
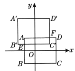
【题目】如图,长方形ABCD各顶点分别为A(-2,2),B(-2,-1),C(3,-1),D(3,2),如果长方A'B'C'D'先向右平移1个单位长度,再向下平移2个单位长度,恰能与长方形ABCD完全重合.
(1)求长方形A'B'C'D'各顶点的坐标;
(2)如果线段AB与线段B'C'交于点E,线段AD与线段C'D'交于点F,求点E,F的坐标.
【答案】(1) A'(-3,4),B'(-3,1),C'(2,1),D'(2,4);(2) E(-2,1), F(2,2).
【解析】
(1)根据平移中,点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减.即可得出平移后点的坐标;
(2)根据与y轴平行的直线上点的横坐标相等,与x轴平行的直线上点的纵坐标相等,即可得到点E,F的坐标.
(1)由已知得,长方形ABCD先向上平移2个单位长度,再向左平移1个单位长度后得到长方形A'B'C'D',
则A'(-3,4),B'(-3,1),C'(2,1),D'(2,4);
(2)∵AE∥y轴,
∴点A、E的横坐标相等,
∵EC'∥x轴,
∴点E、C'的纵坐标相等,即点E的坐标为(-2,1),
∵C'F∥y轴,
∴点C'、F的横坐标相等,均为2,
又∵AF∥x轴,
∴点A、F的纵坐标相等均为2,
即点F(2,2).

练习册系列答案
相关题目