题目内容
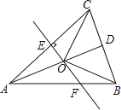
【题目】已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
(1)如图1,点D在AC上,求证:∠BGC=∠BAC;
(2)如图2,当点D不在AC上,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
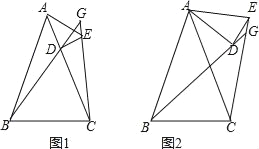
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
试题此题考查全等三角形的判定和性质,关键是证明△AEC≌△ADB.
(1)证△ABD和△ACE全等得出∠ABD=∠ACE,又∠ADB=∠GDC,证明∠BGC=∠BAC即可;
(2)先证△AEC≌△ADB,则有∠ABG=∠ACE,再加上对顶角相等;得出∠BGC=∠BAC即可.
试题解析:证明:(1)在△ABD和△ACE中,
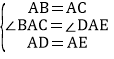 ,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠ADB=∠GDC,
∴∠BGC=∠BAC;
(2)成立,理由如下:
在△AEC与△ADB中,
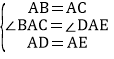 ,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠ADB=∠GDC,
∴∠BGC=∠BAC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目