题目内容
12、(1)如图①,A,B,C三点在一直线上,分别以AB,BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G.则AE=DC吗?BF=BG吗?请说明理由;
(2)如图②,若A,B,C不在同一直线上,那么这时上述结论成立吗?若成立请证明;
(3)在图①中,若连接F,G,你还能得到什么结论?(写出结论,不需证明)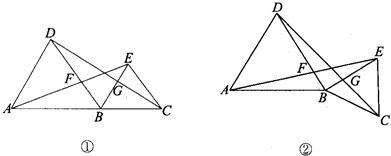
(2)如图②,若A,B,C不在同一直线上,那么这时上述结论成立吗?若成立请证明;
(3)在图①中,若连接F,G,你还能得到什么结论?(写出结论,不需证明)

分析:只需找出两个三角形全等的条件即可证明.
解答:解:AE=DC,BF=BG.理由如下:
(1)因为△ABD,△BCE是等边三角形,
∴AB=DB,EB=BC,∠ABD+∠EBD=∠EBC+EBD,
故△ABE≌△DBC(SAS);
所以AE=DC,∠BAE=∠BDC,
AB=BD,
∠ABD=∠DBE=60°
∴△ABF≌△DBG,
∴BF=BG.
(2)AE=DC仍成立,理由同上,
因为始终有△ABE≌△DBC(SAS);
而BF=BG不成立.
(3)FG∥AC.
(1)因为△ABD,△BCE是等边三角形,
∴AB=DB,EB=BC,∠ABD+∠EBD=∠EBC+EBD,
故△ABE≌△DBC(SAS);
所以AE=DC,∠BAE=∠BDC,
AB=BD,
∠ABD=∠DBE=60°
∴△ABF≌△DBG,
∴BF=BG.
(2)AE=DC仍成立,理由同上,
因为始终有△ABE≌△DBC(SAS);
而BF=BG不成立.
(3)FG∥AC.
点评:本题考查了全等三角形的判定和性质;三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.