��Ŀ����
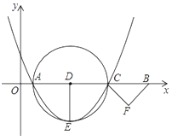
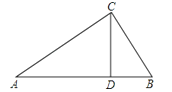
����Ŀ����1����ͼ1����֪������ABC�У�AB=AC=10��BDƽ����ABC��CDƽ����ACB������D��EF��BC���ֱ�AB��AC��E��F���㣬��ͼ�й���__________�����������Σ�EF��BE��CF֮���������ϵ��__________����AEF���ܳ���__________��
��2����ͼ2��������1��������ABC�У�AB=AC=10����Ϊ������ABCΪ���ȱ������Σ�AB=8��AC=10�������������䣬��ͼ�й���__________�����������Σ�EF��BE��CF֮���������ϵ��ʲô��֤����Ľ��ۣ��������AEF���ܳ���
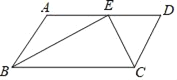
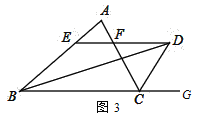
��3����֪����ͼ3��D����ABC�⣬AB>AC����BDƽ����ABC��CDƽ����ABC�������ACG������D��DE��BC���ֱ�AB��AC��E��F���㣬��EF��BE��CF֮�����к�������ϵ�أ�ֱ��д�����۲�֤����

���𰸡���1��5��BE+CF=EF��20�� ��2��2��BE+CF=EF��֤������������AEF���ܳ�=18����3��BE-CF=EF�����ɼ�����.
�������������������1�����ݽ�ƽ���ߵĶ���ɵ���EBD=��CBD����FCD=��BCD���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵ���EDB=��CBD����FDC=��BCD��Ȼ�������EBD=��EDB����FDC=��BCD���ٸ��ݵȽǶԵȱ߿ɵ�BE=DE��CF=DF��Ȼ���ɣ�
��2�����ݽ�ƽ���ߵĶ���ɵ���EBD=��CBD����FCD=��BCD���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵ���EDB=��CBD����FDC=��BCD��Ȼ�������EBD=��EDB����FDC=��BCD���ٸ��ݵȽǶԵȱ߿ɵ�BE=DE��CF=DF��Ȼ���ɣ�
��3���ɣ�2��֪BE=ED��CF=DF��Ȼ�����õ�����������֤��BE��CF��EF��������������ϵ��
����������⣺��1��BE+CF=EF���������£�
��AB=AC�����ABC=��ACB����BDƽ����ABC��CDƽ����ACB�����EBD=��CBD����FCD=��BCD�����DBC=��DCB����DB=DC��
��EF��BC�����AEF=��ABC����AFE=��ACB����EDB=��CBD����FDC=��BCD�����EBD=��EDB����FDC=��BCD����BE=DE��CF=DF��AE=AF������������������ABC����AEF����DEB����DFC����BDC��5������BE+CF=DE+DF=EF����BE+CF=EF����AEF���ܳ�=AE+EF+AF=AE+BE+AF+FC=AB+AC=20��
�ʴ�Ϊ��5��BE+CF=EF��20��
��2��BE+CF=EF����BDƽ����ABC��CDƽ����ACB�����EBD=��CBD����FCD=��BCD����EF��BC�����EDB=��CBD����FDC=��BCD�����EBD=��EDB����FDC=��BCD����BE=DE��CF=DF������������������BDE����CFD����BE+CF=DE+DF=EF����BE+CF=EF����AEF���ܳ�=AE+EF+AF=AE+ED+DF+AF=AE+EB+CF+AF=AB+AC=8+10=18��
��ʱ���������������Σ�EF��BE��CF��C��AEF��18��
��3��BE��CF=EF���ɣ�1��֪BE=ED����EF��BC�����EDC=��DCG=��ACD����CF=DF������ED��DF=EF����BE��CF=EF��