题目内容
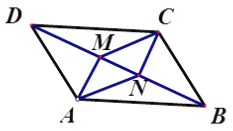
【题目】如图,在平行四边形ABCD中,AM、CN都是BD的垂线,M、N是垂足.
求证:(1)AM=CN;(2)∠MAN=∠NCM.
【答案】证明见解析.
【解析】试题分析:(1)根据平行四边形的性质可证AD=BC,∠ADB=∠CBD,由垂直的定义得∠AMD=∠BNC=90,根据“AAS”可证△ADM≌△BCN;
(2)由(1)知AM=CN,又由AM、CN都是BD的垂线,可得AM∥BN,从而可证四边形AMCN是平行四边形.
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD.
∵AM、CN都是BD的垂线,
∴∠AMD=∠BNC=90.
在△ADM和△BCN中,
∵∠ADB=∠CBD,
∠AMD=∠BNC,
AD=BC,
∴△ADM≌△BCN,
∴AM=CN;
(2)∵AM、CN都是BD的垂线,
∴AM∥CN;
由(1)得,
AM=CN;
∴四边形AMCN是平行四边形
∴∠MAN=∠NCM.

练习册系列答案
相关题目