Question

【题目】如图，在平面直角坐标系中，点A（1，0）、B（11，0），点C为线段AB上一动点，以AC为直径的⊙D的半径DE⊥AC，△CBF是以CB为斜边的等腰直角三角形，且点E、F都在第四象限，当点F到过点A、C、E三点的抛物线的顶点的距离最小时，该抛物线的解析式为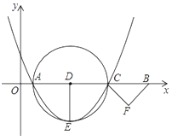

Answer 1

【答案】y=（x﹣）2﹣
【解析】解：设点C（m，0），
∵以AC为直径的⊙D的半径DE⊥AC，
∴点
∵△CBF是以CB为斜边的等腰直角三角形，
∴ ，
∴ ，
当点F到过点A、C、E三点的抛物线的顶点的距离最小，
∴当m=6时，EF最小=6，
∴C（6，0），E（ ， ﹣），
设抛物线的解析式为y=a（x﹣）2﹣ ，
∵抛物线经过A（1，0），
∴0=a（1﹣）2﹣ ，
∴a= ，
∴y=（x﹣）2﹣ ．
所以答案是y=（x﹣）2﹣ ．