题目内容
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2 , 请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
【答案】
(1)
解:∵抛物线的对称轴为x=1,
∴x=﹣ ![]() =﹣
=﹣ ![]() =1.
=1.
解得:m=1.
∴抛物线的解析式为y=﹣x2+2x
(2)
解:将x=3代入抛物线的解析式得y=﹣32+2×3=﹣3.
将y=﹣3代入得:﹣x2+2x=﹣3.
解得:x1=﹣1,x2=3.
∵a=﹣1<0,
∴当n<﹣1或n>3时,y1<y2
(3)
解:设点M关于y轴对称点为M′,则点M′运动的轨迹如图所示:
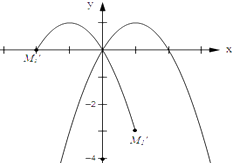
∵当P=﹣1时,q=﹣(﹣1)2+2×(﹣1)=﹣3.
∴点M关于y轴的对称点M1′的坐标为(1,﹣3).
∵当P=2时,q=﹣22+2×2=0,
∴点M关于y轴的对称点M2′的坐标为(﹣2,0).
①当k<0时,
∵点M关于y轴的对称点都在直线y=kx﹣4的上方,
∴﹣2k﹣4≤0.
解得:k≥﹣2.
②当k>0时,
∵点M关于y轴的对称点都在直线y=kx﹣4的上方,
∴k﹣4≤﹣3.
解得;k≤1.
∴k的取值范围是﹣2≤k≤1
【解析】(1)由抛物线的对称轴方程可求得m=1,从而可求得抛物线的表达式;(2)将x=3代入抛物线的解析式,可求得y2=3,将y=3代入抛物线的解析式可求得x1=﹣1,x2=3,由抛物线的开口向下,可知当当n<﹣1或n>3时,y1<y2;(3)先根据题意画出点M关于y轴对称点M′的轨迹,然后根据点M关于y轴的对称点都在直线y=kx﹣4的上方,列出关于k的不等式组即可求得k的取值范围.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从表可知,
①抛物线与x轴的交点为;
②抛物线的对称轴是;
③函数y=ax2+bx+c的最大值为;
④x , y随x增大而增大.