ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΓςABCΚΆΓςADE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœACBΘΫΓœADEΘΫ90ΓψΘ§FΈΣBEΒΡ÷–ΒψΘ§Ν§ΫαDFΘ§CF.
(1)»γΆΦΔΌΘ§Β±ΒψD‘ΎAB…œΘ§ΒψE‘ΎAC…œΘ§«κ÷±Ϋ”–¥≥ω¥Υ ±œΏΕΈDFΘ§CFΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΘ°
(2)»γΆΦΔΎΘ§‘Ύ(1)ΒΡΧθΦΰœ¬ΫΪΓςADE»ΤΒψAΥ≥ ±’κ–ΐΉΣ45ΓψΘ§«κΡψ≈–Εœ¥Υ ±(1)÷–ΒΡΫα¬έ «Ζώ»‘»Μ≥…ΝΔΘ§≤Δ÷ΛΟςΡψΒΡ≈–ΕœΘ°
(3)»γΆΦΔέΘ§‘Ύ(1)ΒΡΧθΦΰœ¬ΫΪΓςADE»ΤΒψAΥ≥ ±’κ–ΐΉΣ90ΓψΘ§»τADΘΫ1Θ§ACΘΫ2![]() Θ§«σ¥Υ ±œΏΕΈCFΒΡ≥Λ(÷±Ϋ”–¥≥ωΫαΙϊ)Θ°
Θ§«σ¥Υ ±œΏΕΈCFΒΡ≥Λ(÷±Ϋ”–¥≥ωΫαΙϊ)Θ°

ΓΨ¥πΑΗΓΩ(1)÷ΛΟςΦϊΫβΈω(2)(1)÷–ΒΡΫα¬έ»‘»Μ≥…ΝΔ(3) ![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΓΑ÷±Ϋ«»ΐΫ«–Έ–±±Ώ…œΒΡ÷–œΏΒ»”Ύ–±±ΏΒΡ“ΜΑκΓ±Ω…÷ΣDF=BFΘ§ΗυΨίΓœDFE=2ΓœDCFΘ§ΓœBFE=2ΓœBCFΘ§ΒΟΒΫΓœEFD+ΓœEFB=2ΓœDCB=90ΓψΘ§DFΓΆBFΘ°
Θ®2Θ©―”≥ΛDFΫΜBC”ΎΒψGΘ§œ»÷ΛΟςΓςDEFΓ’ΓςGCFΘ§ΒΟΒΫDE=CGΘ§DF=FGΘ§ΗυΨίAD=DEΘ§AB=BCΘ§ΒΟΒΫBD=BG”÷“ρΈΣΓœABC=90ΓψΘ§Υυ“‘DF=CF«“DFΓΆBFΘ°
Θ®3Θ©―”≥ΛDFΫΜBA”ΎΒψHΘ§œ»÷ΛΟςΓςDEFΓ’ΓςHBFΘ§ΒΟΒΫDE=BHΘ§DF=FHΘ§ΗυΨί–ΐΉΣΧθΦΰΩ…“‘ΓςADHΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§”…ΓςABCΚΆΓςADE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§AC=2![]() Θ§Ω…“‘«σ≥ωABΒΡ÷ΒΘ§ΫχΕχΩ…“‘ΗυΨίΙ¥Ι…Ε®άμΩ…“‘«σ≥ωDHΘ§‘Ό«σ≥ωDFΘ§”…DF=BFΘ§«σ≥ωΒΟCFΒΡ÷ΒΘ°
Θ§Ω…“‘«σ≥ωABΒΡ÷ΒΘ§ΫχΕχΩ…“‘ΗυΨίΙ¥Ι…Ε®άμΩ…“‘«σ≥ωDHΘ§‘Ό«σ≥ωDFΘ§”…DF=BFΘ§«σ≥ωΒΟCFΒΡ÷ΒΘ°
‘ΧβΫβΈωΘΚ(1)ΓΏΓœACB=ΓœADE=90ΓψΘ§FΈΣBEΒΡ÷–ΒψΘ§
ΓύDF=BF=![]() BEΘ§CF=
BEΘ§CF=![]() BEΘ§ΓύDF=CF.
BEΘ§ΓύDF=CF.
ΓΏΓςABC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓύΓœABC=45Γψ.
ΓΏBF=DFΘ§ΓύΓœDBF=ΓœBDF.
ΓΏΓœDFE=ΓœDBFΘΪΓœBDFΘ§
ΓύΓœDFE=2ΓœDBF.
Ά§άμΘ§ΓœCFE=2ΓœCBFΘ§
ΓύΓœDFEΘΪΓœCFE=2ΓœDBFΘΪ2ΓœCBF=2ΓœABC=90ΓψΘ§ΓύDFΓΆCF.
(2)(1)÷–ΒΡΫα¬έ»‘»Μ≥…ΝΔΘ°
÷ΛΟςΘΚ»γΫβΆΦΔΌΘ§―”≥ΛDFΫΜBC”ΎΒψG.
ΓΏΓœADE=ΓœACB=90ΓψΘ§ΓύDEΓΈBC.
ΓύΓœDEF=ΓœGBFΘ§ΓœEDF=ΓœBGF.
ΓΏFΈΣBEΒΡ÷–ΒψΘ§ΓύEF=BF.
ΓύΓςDEFΓ’ΓςGBF(AAS)Θ°ΓύDE=GBΘ§DF=GF.
ΓΏAD=DEΘ§ΓύAD=GB.
ΓΏAC=BCΘ§ΓύACΘ≠AD=BCΘ≠GBΘ§
Φ¥DC=GC.
ΓΏΓœACB=90ΓψΘ§ΓύΓςDCG «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ°
ΓΏDF=GFΘ§ΓύDF=CFΘ§DFΓΆCF.
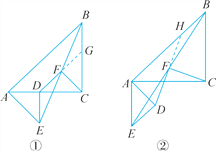
(3)»γΫβΆΦΔΎΘ§―”≥ΛDFΫΜBA”ΎΒψH.
ΓΏΓςABCΚΆΓςADE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύAC=BCΘ§AD=DEΘ§
ΓœAED=ΓœABC=45Γψ.
”…–ΐΉΣΩ…÷ΣΓœCAE=ΓœBAD=ΓœACB=90ΓψΘ§
ΓύAEΓΈBCΘ§
ΓύΓœAEB=ΓœCBEΘ§ΓύΓœDEF=ΓœHBF.
ΓΏF «BEΒΡ÷–ΒψΘ§ΓύEF=BF.
”÷ΓΏΓœDFE=ΓœHFBΘ§
ΓύΓςDEFΓ’ΓςHBF(ASA)Θ°ΓύED=BH.
ΓΏBC=AC=2![]() Θ§ΓœACB=90ΓψΘ§ΓύAB=4.
Θ§ΓœACB=90ΓψΘ§ΓύAB=4.
ΓΏBH=ED=AD=1Θ§ΓύAH=3.
ΓΏΓœBAD=90ΓψΘ§ΓύDH=![]() Θ§
Θ§
ΓύDF=![]()
.ΓύCF=![]() .
.

