Question

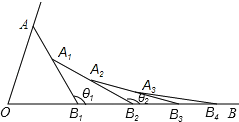
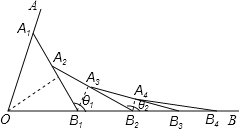
【题目】如图所示，已知∠AOB=α，在射线OA、OB上分别取点OA1=OB1，连结A1B1，在B1A1、B1B上分别取点A2、B2，使B1B2=B1A2，连结A2B2…按此规律下去，记∠A2B1 B2=θ1，∠A3B2B3=θ2，…，∠An+1Bn Bn+1=θn，则θ2016﹣θ2015的值为（ ）

A． B． C． D．

Answer 1

【答案】D

【解析】

试题分析：根据等腰三角形两底角相等用α表示出∠A1B1O，再根据平角等于180°列式用α表示出θ1，再用θ1表示出θ2，并求出θ2﹣θ1，依此类推求出θ3﹣θ2，…，θ2013﹣θ2012，即可得解．

解：∵OA1=OB1，∠AOB=α，

∴∠A1B1O=（180°﹣α），

∴（180°﹣α）+θ1=180，

整理得，θ1=，

∵B1B2=B1A2，∠A2B1B2=θ1，

∴∠A2B2B1=（180°﹣θ1），

∴（180°﹣θ1）+θ2=180°，

整理得θ2==，

∴θ2﹣θ1=﹣==，

同理可求θ3==，

∴θ3﹣θ2=﹣==，

…，

依此类推，θ2016﹣θ2015=．

故选D．