题目内容
 (2009•西藏)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
(2009•西藏)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.(1)试探究AD和CD的位置关系,并说明理由.
(2)若AD=3,AC=
| 15 |
分析:(1)连接OC,由于CD是切线,那么∠DCO=∠DCA+∠ACO=90°,而OA=OC,于是∠OAC=∠ACO,再结合AC是∠DAB平分线,易知∠DAC=∠OAC,从而有∠DAC=∠ACO,于是∠DCA+∠DAC=90°,即可证AD⊥CD;
(2)连接BC,由(1)知∠DAC=∠BAC,而∠ADC=∠ACB=90°,易证△ADC∽△ACB,利用比例线段,易求AB.
(2)连接BC,由(1)知∠DAC=∠BAC,而∠ADC=∠ACB=90°,易证△ADC∽△ACB,利用比例线段,易求AB.
解答: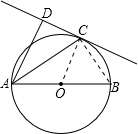 解:(1)AD⊥CD.理由如下:连接OC.
解:(1)AD⊥CD.理由如下:连接OC.
∵直线CD与⊙O相切于点C,
∴∠DCO=∠DCA+∠ACO=90°,
∵AO=CO,
∴∠OAC=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠ACO,
∴∠DCA+∠DAC=90°,
∴∠ADC=90°,
即AD⊥CD;
(2)连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
=
.
∵AD=3,AC=
,
∴AB=5.
 解:(1)AD⊥CD.理由如下:连接OC.
解:(1)AD⊥CD.理由如下:连接OC.∵直线CD与⊙O相切于点C,
∴∠DCO=∠DCA+∠ACO=90°,
∵AO=CO,
∴∠OAC=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠ACO,
∴∠DCA+∠DAC=90°,
∴∠ADC=90°,
即AD⊥CD;
(2)连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
| AD |
| AC |
| AC |
| AB |
∵AD=3,AC=
| 15 |
∴AB=5.
点评:本题考查了切线的性质、圆周角定理、角平分线定义、相似三角形的判定和性质.解题的关键是连接OC、BC,构造等腰三角形、直角三角形,并证明∠DAC=∠ACO.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009•西藏)如图,已知a∥b,∠1=50°,那么∠2的度数是( )
(2009•西藏)如图,已知a∥b,∠1=50°,那么∠2的度数是( )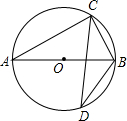 (2009•西藏)如图,AB是圆O的直径,点C、D在圆O上,∠ABC=65°,则∠D的度数是( )
(2009•西藏)如图,AB是圆O的直径,点C、D在圆O上,∠ABC=65°,则∠D的度数是( ) (2009•西藏)如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为( )
(2009•西藏)如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为( ) (2009•西藏)如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE:BC的值为
(2009•西藏)如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE:BC的值为