题目内容
（2009•西藏）如图，在△ABC中，DE∥BC，DE分别与AB、AC相交于点D、E，若AD=4，DB=2，则DE：BC的值为2：3
2：3
．分析：由AD=4，DB=2，即可求得AB的长，又由DE∥BC，根据平行线分线段成比例定理，可得DE：BC=AD：AB，则可求得答案．
解答：解：∵AD=4，DB=2，
∴AB=AD+BD=4+2=6，
∵DE∥BC，
∴DE：BC=AD：AB=4：6=2：3．
故答案为2：3．
∴AB=AD+BD=4+2=6，
∵DE∥BC，
∴DE：BC=AD：AB=4：6=2：3．
故答案为2：3．
点评：此题考查了平行线分线段成比例定理．此题比较简单，注意掌握比例线段的对应关系是解此题的关键．
练习册系列答案
相关题目
（2009•西藏）如图，已知a∥b，∠1=50°，那么∠2的度数是（ ）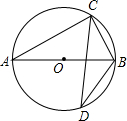
（2009•西藏）如图，AB是圆O的直径，点C、D在圆O上，∠ABC=65°，则∠D的度数是（ ）
（2009•西藏）如图，在菱形ABCD中，已知AB=10，AC=16，那么菱形ABCD的面积为（ ）
（2009•西藏）如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．