题目内容
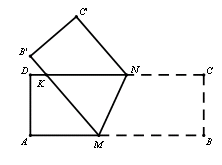
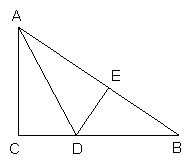
如图,C为线段BD上一动点,分别过点B,D作AB BD,ED
BD,ED BD,连接AC,ED。已知AB=5,DE=1,BD=8,设CD=x。
BD,连接AC,ED。已知AB=5,DE=1,BD=8,设CD=x。
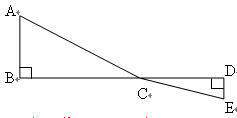
(1)用含的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构造图形(给出必要的说明)求出代数式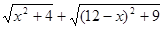 的最小值。
的最小值。
 BD,ED
BD,ED BD,连接AC,ED。已知AB=5,DE=1,BD=8,设CD=x。
BD,连接AC,ED。已知AB=5,DE=1,BD=8,设CD=x。
(1)用含的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构造图形(给出必要的说明)求出代数式
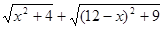 的最小值。
的最小值。(1)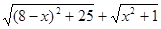 ………………3分.
………………3分.
(2)解:当点C为AE和BD的交点时,根据两点之间线段最短,所以AC+CE的值最小………………3分
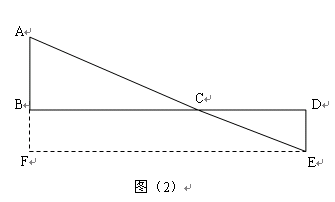
(3)解:如图(1),C为线段BD上一动点,分别过点B,D作AB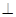 BD,ED
BD,ED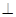 BD,连接AC, ED。已知AB=3,DE=2,BD=12,设CD=x。………………2分
BD,连接AC, ED。已知AB=3,DE=2,BD=12,设CD=x。………………2分

如图(2),当点C为AE和BD交点时,代数式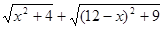 的值最小,过点E作EF
的值最小,过点E作EF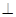 AB,垂足为点F,所以四边形BFED为矩形,BF=DE=2,
AB,垂足为点F,所以四边形BFED为矩形,BF=DE=2,
在Rt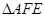 中,AF=5,EF=12,
中,AF=5,EF=12,
AE=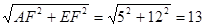 ,所以,代数式
,所以,代数式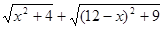 的值最小为13。……………………6分
的值最小为13。……………………6分
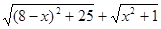 ………………3分.
………………3分.(2)解:当点C为AE和BD的交点时,根据两点之间线段最短,所以AC+CE的值最小………………3分
(3)解:如图(1),C为线段BD上一动点,分别过点B,D作AB
 BD,ED
BD,ED BD,连接AC, ED。已知AB=3,DE=2,BD=12,设CD=x。………………2分
BD,连接AC, ED。已知AB=3,DE=2,BD=12,设CD=x。………………2分
如图(2),当点C为AE和BD交点时,代数式
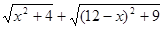 的值最小,过点E作EF
的值最小,过点E作EF AB,垂足为点F,所以四边形BFED为矩形,BF=DE=2,
AB,垂足为点F,所以四边形BFED为矩形,BF=DE=2,在Rt
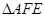 中,AF=5,EF=12,
中,AF=5,EF=12,AE=
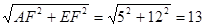 ,所以,代数式
,所以,代数式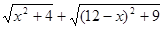 的值最小为13。……………………6分
的值最小为13。……………………6分
(1)利用勾股定理求解
(2)根据两点之间线段最短解答
(3)分别过点B,D作AB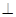 BD,ED
BD,ED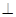 BD,连接AC, ED,过点E作EF
BD,连接AC, ED,过点E作EF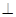 AB,垂足为点F,得四边形BFED为矩形,利用勾股定理求解
AB,垂足为点F,得四边形BFED为矩形,利用勾股定理求解
(2)根据两点之间线段最短解答
(3)分别过点B,D作AB
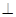 BD,ED
BD,ED BD,连接AC, ED,过点E作EF
BD,连接AC, ED,过点E作EF AB,垂足为点F,得四边形BFED为矩形,利用勾股定理求解
AB,垂足为点F,得四边形BFED为矩形,利用勾股定理求解
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
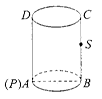
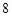 cm,高为
cm,高为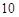 cm. 动点
cm. 动点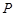 从
从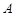 点出发,沿圆柱的侧面移动到
点出发,沿圆柱的侧面移动到 的中点
的中点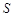 的最短距离是 cm(
的最短距离是 cm(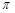 取
取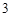 ).
).
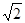 ,AB=
,AB=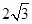 ,那么sin∠ACD的值是
,那么sin∠ACD的值是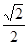
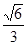
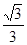
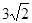 m。求点B到地面的垂直距离BC.
m。求点B到地面的垂直距离BC.
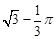
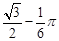
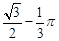
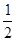
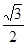
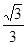
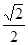
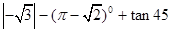 º
º