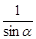题目内容
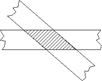
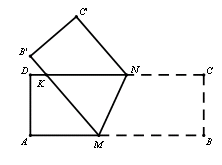
如图,矩形纸片ABCD,AD=BC=3,AB=CD=9,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK,则对△MNK的叙述正确的个数是:①△MNK一定是等腰三角形;②△MNK可能是钝角三角形;③△MNK有最小面积且等于4.5;④△MNK有最大面积且等于7.5

| A.1个 | B.2个 | C.3个 | D.4个 |
D
本题主要考查了矩形和翻折的性质.
①△MNK一定是等腰三角形;由于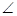 KMN=
KMN=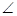 BMN,
BMN,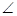 KNM=
KNM=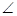 KMN,所以MK=NK,故成立。
KMN,所以MK=NK,故成立。
②△MNK可能是钝角三角形;当点K距离CD边上点C很近时,就是钝角三角形,成立。
④△MNK有最大面积且等于7.5,因为将矩形纸片对折,使点B与点D重合,此时点K与点D重合,设MK=MD=X,则AM=9-x,由勾股定理可知,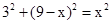 ,解得x=5,故△MNK有最大面积
,解得x=5,故△MNK有最大面积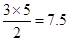 。成立。
。成立。
③△MNK有最小面积且等于4.5;类比上述原理可知满足题意。
故选D.
①△MNK一定是等腰三角形;由于
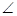 KMN=
KMN= BMN,
BMN,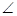 KNM=
KNM=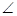 KMN,所以MK=NK,故成立。
KMN,所以MK=NK,故成立。②△MNK可能是钝角三角形;当点K距离CD边上点C很近时,就是钝角三角形,成立。
④△MNK有最大面积且等于7.5,因为将矩形纸片对折,使点B与点D重合,此时点K与点D重合,设MK=MD=X,则AM=9-x,由勾股定理可知,
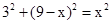 ,解得x=5,故△MNK有最大面积
,解得x=5,故△MNK有最大面积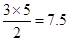 。成立。
。成立。③△MNK有最小面积且等于4.5;类比上述原理可知满足题意。
故选D.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
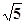 的对应的点。
的对应的点。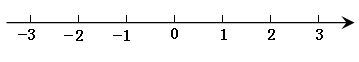
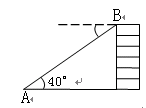
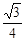 ,求锐角α.
,求锐角α.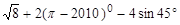 .
.
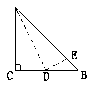
 BD,ED
BD,ED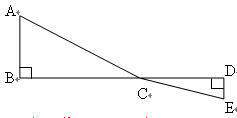
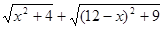 的最小值。
的最小值。