题目内容
顺次连接等腰梯形各边中点得到的四边形是_____________。
菱形
连接AC、BD,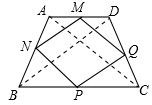
∵M、N分别为AD、AB的中点
∴MN为△ABD的中位线,∴MN∥BD,MN=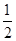 BD,
BD,
同理可证BD∥PQ,PQ=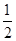 BD,
BD,
∴MN=PQ,MN∥PQ,四边形PQMN为平行四边形,
同理可证NP=MQ=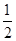 AC,
AC,
根据等腰梯形的性质可知AC=BD,
∴PQ=NP,
∴?PQMN为菱形.

∵M、N分别为AD、AB的中点
∴MN为△ABD的中位线,∴MN∥BD,MN=
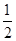 BD,
BD,同理可证BD∥PQ,PQ=
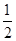 BD,
BD,∴MN=PQ,MN∥PQ,四边形PQMN为平行四边形,
同理可证NP=MQ=
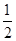 AC,
AC,根据等腰梯形的性质可知AC=BD,
∴PQ=NP,
∴?PQMN为菱形.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
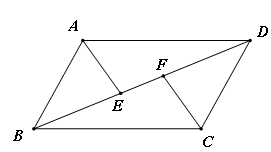
 AC•BD;
AC•BD;
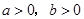 ,则
,则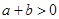 ;②正方形的对角线互相垂直平分;③直角三角形斜边上的中线等于斜边的一半;④菱形的四条边相等.其中原命题与逆命题均为真命题的个数是( )
;②正方形的对角线互相垂直平分;③直角三角形斜边上的中线等于斜边的一半;④菱形的四条边相等.其中原命题与逆命题均为真命题的个数是( )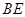 平分
平分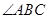 ,交
,交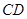 于点
于点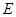 ,点
,点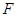 在边
在边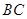 上.
上.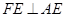 ,那么
,那么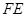 和
和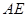 相等吗?证明你的结论.
相等吗?证明你的结论.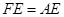 ,那么
,那么