题目内容
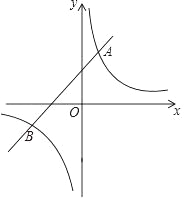
【题目】如图，直线y1=x+2与双曲线y2=
交于A（a，4），B（m，n）．
（1）求k值和点B的坐标；
（2）求△AOB的面积；
（3）当y1＞y2时请直接写出x的取值范围；
（4）P为x轴上任意一点，当△ABP为直角三角形时，直接写出P点坐标．
【答案】（1）8（2）点B（﹣4，﹣2）（3）﹣4＜x＜0或x＞2（4）当△ABP为直角三角形时，P点坐标为（﹣1﹣
，0）、（﹣1+
，0）、（﹣6，0）或（6，0）
【解析】试题分析：（1）由点A在直线上可求出a，从而得出点A的坐标，由点A在反比例函数图象上即可求出k值；
（2）联立直线与双曲线的解析式成方程组，解方程组即可求出点B的坐标；
（3）根据函数图象的上下位置关系结合交点坐标即可得出结论；
（4）设点P的坐标为（m，0），由两点间的距离公式求出AP、AB、BP，分AP、AB、BP为斜边来考虑，根据勾股定理得出关于m的方程，解方程即可得出结论．
试题解析：解：（1）∵点A（a，4）在直线y1=x+2上，∴4=a+2，解得：a=2，∴点A（2，4）．∵点A（2，4）在双曲线
上，∴k=2×4=8．
（2）联立直线与双曲线解析式成方程组得：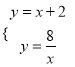 
，解得： 
， 
，∴点B（﹣4，﹣2）．
（3）观察函数图象，发现：当﹣4＜x＜0或x＞2时，直线在双曲线的上方，∴当y1＞y2时x的取值范围为﹣4＜x＜0或x＞2．
（4）设点P的坐标为（m，0），则AB2=
=72，AP2=
，BP2=
，△ABP为直角三角形分三种情况：
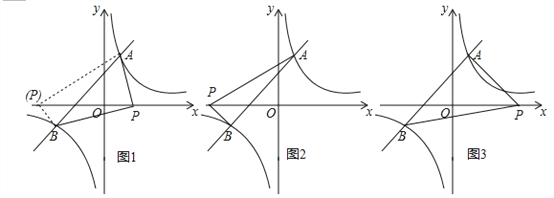
①AB为斜边时（图1），有AB2=AP2+BP2，即72=（m﹣2）2+16+（m+4）2+4，解得：m1=﹣1﹣
，m2=﹣1+
，此时点P坐标为（﹣1﹣
，0）或（﹣1+
，0）；
②AP为斜边时（图2），有AP2=AB2+BP2，即（m﹣2）2+16=72+（m+4）2+4，解得：m3=﹣6，此时点P坐标为（﹣6，0）；
③BP为斜边时（图3），有BP2=AB2+AP2，即（m+4）2+4=72+（m﹣2）2+16，解得：m4=6，此时点P坐标为（6，0）．
综上可知：当△ABP为直角三角形时，P点坐标为（﹣1﹣
，0）、（﹣1+
，0）、（﹣6，0）或（6，0）．
