题目内容
如图，在直角坐标系中，将矩形OABC绕O点逆时针旋转30°，使点B落在点B′处，已知OA=| 3 |
（1，
）
| 3 |
（1，
）
．| 3 |
分析：根据旋转的性质得出tan∠BOA=
=
，OA′=
，A′B′=1，∠B′OB=30°，进而得出∠B′ON=60°，进而利用锐角三角函数关系得出B′N，NO的长即可得出点B′的坐标．
| AB |
| OA |
| ||
| 3 |
| 3 |
解答：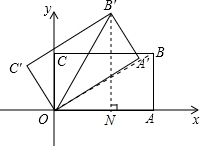
解：连接OB，OB′，过点B′作B′N⊥x轴于点N，
∵将矩形OABC绕O点逆时针旋转30°，使点B落在点B′处，OA=
，AB=1，
∴tan∠BOA=
=
，OA′=
，A′B′=1，∠B′OB=30°，
∴∠BOA=∠B′OA′=30°，OB=OB′=2
∴∠B′ON=60°，
∴sin60°=
=
=
，
∴B′N=
，
∴NO=
=1，
∴点B′的坐标是：（1，
）．
故答案为：（1，
）．
解：连接OB，OB′，过点B′作B′N⊥x轴于点N，∵将矩形OABC绕O点逆时针旋转30°，使点B落在点B′处，OA=
| 3 |
∴tan∠BOA=
| AB |
| OA |
| ||
| 3 |
| 3 |
∴∠BOA=∠B′OA′=30°，OB=OB′=2
∴∠B′ON=60°，
∴sin60°=
| B′N |
| OB′ |
| B′N |
| 2 |
| ||
| 2 |
∴B′N=
| 3 |
∴NO=
22-(
|
∴点B′的坐标是：（1，
| 3 |
故答案为：（1，
| 3 |
点评：此题主要考查了旋转的性质以及锐角三角函数关系和勾股定理等知识，得出∠B′ON的度数是解题关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：