Question

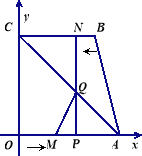
【题目】如图，抛物线y=ax2-2ax+b经过点C（0，-），且与x轴交于点A、点B，若tanACO=．

（1）求此抛物线的解析式；

（2）若抛物线的顶点为M，点P是线段OB上一动点（不与点B重合），MPQ=45，射线PQ与线段BM交于点Q，当△MPQ为等腰三角形时，求点P的坐标．

Answer 1

【答案】（1）y=x2-x-（2）当△MPQ为等腰三角形时，点P的坐标为(1，0)或(3-,0).

【解析】

（1）根据抛物线y=ax2-2ax+b经过点C（0，-），求出b=-，再根据tan∠ACO=，求出点A的坐标，再利用待定系数法即可得出此抛物线的解析式；

（2）由y=x2-x-=(x-1)2-2，可得M(-1,-2)，令y=x2-x-=0，得x1=-1,x2=3，从而可得B(3,0)，如图，作MH⊥OB于点H，则MH=BH=2，可推导得出△MPQ∽△MBP，从而可得当△MPQ为等腰三角形时，△MBP也为等腰三角形，然后分情况进行讨论即可得.

（1）∵C（0，），∴OC=.

∵tanACO=，∴OA=1.∴A(-1，0).

∵点A,C在抛物线y=ax2-2ax+b上，

∴，解得，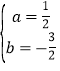

∴此抛物线的解析式为y=x2-x-；

（2）∵y=x2-x-=(x-1)2-2，∴M(-1,-2)，

令y=x2-x-=0，得x1=-1,x2=3，∴B(3,0)，

如图，作MH⊥OB于点H，则MH=BH=2，

∴∠MBO=45=∠MBP，

又∵∠PMQ=∠BMP，∴△MPQ∽△MBP，

∴当△MPQ为等腰三角形时，△MBP也为等腰三角形，

①当MQ=PQ时，PM=BP，∠BMP=∠MBP=45，∠MPB=90，

∴点P与点H重合，即P(1，0)；

②当MQ=MP时，MP=MB，∠MPB=45，∠BMP=90，

∴PH=BH=2，即P(-1，0)（舍去）；

③当MP=PQ时，BP=BM=，

∴P(3-,0)，

综上所述，当△MPQ为等腰三角形时，点P的坐标为(1，0)或(3-,0).