题目内容
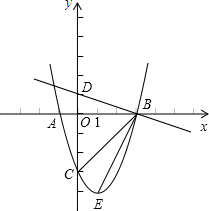 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA,直线y=-
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA,直线y=-| 1 | 3 |
(1)求抛物线的解析式和E点坐标;
(2)求∠DBC-∠CBE的大小;
(3)点F是抛物线第四象限上的点,问四边形OBFC面积最大值为多少?并求此时的点F坐标.
分析:(1)根据抛物线y=ax2+bx-3与y轴交点为(0,-3),求出C(0,-3),再根据OB=OC=3OA,求出A(-1,0),B(3,0),C(0,-3),利用待定系数法求出函数解析式.
(2)作EG⊥CO于G,连CE,易知△OBC、△CEG都是等腰直角三角形,则△CBE是直角三角形.分别在Rt△OBD、Rt△BCE中运用正切定义,得到tanα=
=
;tanβ=
=
=
;判断出则α=β,求出∠DBC-∠CBE=45°.
(3)将S四边形OCFB=转化为S△OCF与S△OBF的和,设出F坐标,利用面积公式将面积转化为二次函数求最值.
(2)作EG⊥CO于G,连CE,易知△OBC、△CEG都是等腰直角三角形,则△CBE是直角三角形.分别在Rt△OBD、Rt△BCE中运用正切定义,得到tanα=
| OD |
| OB |
| 1 |
| 3 |
| CE |
| BC |
| ||
3
|
| 1 |
| 3 |
(3)将S四边形OCFB=转化为S△OCF与S△OBF的和,设出F坐标,利用面积公式将面积转化为二次函数求最值.
解答: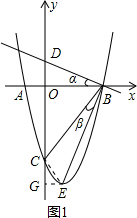 解:(1)∵抛物线y=ax2+bx-3与y轴交点为(0,-3),
解:(1)∵抛物线y=ax2+bx-3与y轴交点为(0,-3),
又∵OB=OC=3OA,
∴A(-1,0),B(3,0),C(0,-3).
将A(-1,0),B(3,0)分别代入y=ax2+bx-3得,
,
解得
,
故函数解析式为y=x2-2x-3,
配方得y=(x-1)2-4,
可得,E(1,-4).
(2)如图1,作EG⊥CO于G,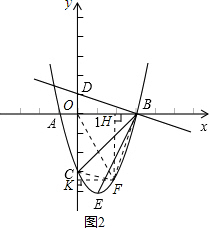 连CE,易知△OBC、△CEG都是等腰直角三角形,
连CE,易知△OBC、△CEG都是等腰直角三角形,
则△CBE是直角三角形.
分别在Rt△OBD、Rt△BCE中运用正切定义,
即有tanα=
=
;tanβ=
=
=
;
则α=β,从而可得∠DBC-∠CBE=45°.
(3)作FH⊥x轴于H,FK⊥y轴于K,设F点坐标为(x,x2-2x-3),
S四边形OCFB=S△OCF+S△OBF=
×3x+
×3x[-(x2-2x-3)]=-
(x-
)2+
,面积最大值为
.
此时,x2-2x-3=
-2×
-3=-
,
故F(
,-
).
 解:(1)∵抛物线y=ax2+bx-3与y轴交点为(0,-3),
解:(1)∵抛物线y=ax2+bx-3与y轴交点为(0,-3),又∵OB=OC=3OA,
∴A(-1,0),B(3,0),C(0,-3).
将A(-1,0),B(3,0)分别代入y=ax2+bx-3得,
|
解得
|
故函数解析式为y=x2-2x-3,
配方得y=(x-1)2-4,
可得,E(1,-4).
(2)如图1,作EG⊥CO于G,
 连CE,易知△OBC、△CEG都是等腰直角三角形,
连CE,易知△OBC、△CEG都是等腰直角三角形,则△CBE是直角三角形.
分别在Rt△OBD、Rt△BCE中运用正切定义,
即有tanα=
| OD |
| OB |
| 1 |
| 3 |
| CE |
| BC |
| ||
3
|
| 1 |
| 3 |
则α=β,从而可得∠DBC-∠CBE=45°.
(3)作FH⊥x轴于H,FK⊥y轴于K,设F点坐标为(x,x2-2x-3),
S四边形OCFB=S△OCF+S△OBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 63 |
| 8 |
| 63 |
| 8 |
此时,x2-2x-3=
| 9 |
| 4 |
| 3 |
| 2 |
| 15 |
| 4 |
故F(
| 3 |
| 2 |
| 15 |
| 4 |
点评:本题是二次函数综合题,考查了二次函数的性质、图象、一次函数的性质和图象,二次函数的最值等,有较大难度.

练习册系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).