题目内容
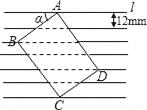
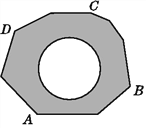
【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1 m的圆后,在封闭图形ABCD附近闭上眼睛向封闭图形内掷小石子(可把小石子近似看成点),
记录如下:
掷小石子所落的总次数 小石子所落的有效区域 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 14 | 48 | 89 | … |
小石子落在圆以外的阴影部分(含外缘)的次数n | 30 | 95 | 180 | … |
(1)当投掷的次数很大时,m∶n的值越来越接近___________(结果精确到0.1);
(2)若以小石子所落的有效区域里的次数为总数(即m+n),则随着投掷次数的增加,小石子落在圆内(含圆上)的频率稳定在___________附近;
(3)若你投一次石子,则小石子落在圆内(含圆上)的概率为___________;
(4)请你利用(2)中所得频率,估计整个封闭图形ABCD的面积是多少平方米(结果保留π).
【答案】(1)0.5;(2)![]() ;(3)
;(3)![]() ;(4)3π m2
;(4)3π m2
【解析】试题分析:根据表格中提供的数据计算出落在圆内的概率与落在阴影内的概率的比值,即可解答.
试题解析:(1)0.5, ![]() ≈0.5,
≈0.5, ![]() ≈0.5,
≈0.5, ![]() ≈0.5,所以m:n的值越来越接近0.5,
≈0.5,所以m:n的值越来越接近0.5,
(2) ![]() 由(1)可得
由(1)可得![]() ≈
≈![]() .
.
(3) ![]()
(4)S圆=π×12=π(m2),而![]() ≈
≈![]() ,
,
所以S封闭图形ABCD≈3π m2.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.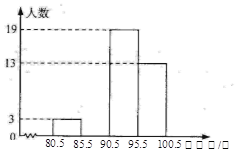
![]()