题目内容
【题目】如图,△ABC中,∠ACB中,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,连接AE.
(1)求证:△ABC≌△AEC;
(2)若AB=AC,试判断四边形ACDE的形状,并说明理由.
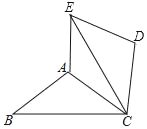
【答案】(1)见解析;(2)四边形ACDE是菱形.理由见解析.
【解析】
(1)根据旋转的性质得出BC=EC,∠ACB=∠DCE=30°,∠BCE=60°,那么∠ACE=30°=∠ACB.再根据SAS即可证明△ABC≌△AEC;
(2)由(1)得△ABC≌△AEC,那么AE=AB,而AB=AC,等量代换得出AE=AB=AC.根据旋转的性质得出△DEC≌△ABC,那么CD=AC=AB,DE=AB,从而得出AC=CD=DE=AE,进而得到四边形ACDE是菱形.
(1)证明:∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴BC=EC,∠ACB=∠DCE=30°,∠BCE=60°,
∴∠ACE=60°﹣30°=30°,
∴∠ACE=∠ACB.
在△ABC与△AEC中,
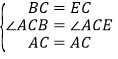
∴△ABC≌△AEC(SAS);
(2)解:四边形ACDE是菱形.理由如下:
由(1)得△ABC≌△AEC,
∴AE=AB,
∴AB=AC,
∴AE=AB=AC.
∵△DEC是由△ABC旋转而得,
∴△DEC≌△ABC,
∴CD=AC=AB,DE=AB,
∴AC=CD=DE=AE,
∴四边形ACDE是菱形.

练习册系列答案
相关题目
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4 分 2,则成绩较为整齐的是 队.