题目内容
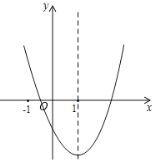
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象交x轴于点A,B(点A在点B的左侧).
的图象交x轴于点A,B(点A在点B的左侧).
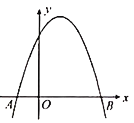
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 的值分别为
的值分别为![]() ,1.
,1.
【解析】
(1)把y=0代入二次函数的解析式中,求得一元二次方程的解便可得A、B两点的坐标,再根据函数图象不在x轴下方的x的取值范围得y≥0时x的取值范围;
(2)根据题意写出B2,B3的坐标,再由对称轴方程列出n的方程,求得n,进而求得m的值.
解:(1)令![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() .
.
由函数图象得,当![]() 时,
时,![]() .
.
(2)由题意得![]() ,
,
函数图象的对称轴为直线![]() .
.
∵点![]() 在二次函数图象上且纵坐标相同,
在二次函数图象上且纵坐标相同,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() 的值分别为
的值分别为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目