��Ŀ����
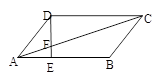
��ͼ����ֱ֪������ABCD�У�AD��BC��AB��BC ��AD��2cm��AB��8cm��CD��10cm��
(1)������ABCD���ܳ���
(2)����P�ӵ�B��������1cm/s���ٶ���B��A��D��C�������C�˶�������Q�ӵ�C��������1cm/s���ٶ���C��D��A�������A�˶�������Q��QF��BC�ڵ�F����P��Q����ͬʱ������������һ�㵽���յ�ʱ�����˶���֮���������˶�ʱ��Ϊt�룮�ʣ�
���˶������У��Ƿ����������t��ʹ����P��D��QΪ�����������ǡ������DQΪһ���ĵ��������Σ������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�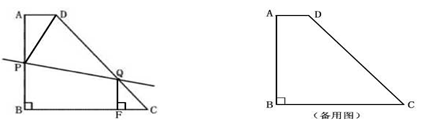
(1)������ABCD���ܳ���
(2)����P�ӵ�B��������1cm/s���ٶ���B��A��D��C�������C�˶�������Q�ӵ�C��������1cm/s���ٶ���C��D��A�������A�˶�������Q��QF��BC�ڵ�F����P��Q����ͬʱ������������һ�㵽���յ�ʱ�����˶���֮���������˶�ʱ��Ϊt�룮�ʣ�
���˶������У��Ƿ����������t��ʹ����P��D��QΪ�����������ǡ������DQΪһ���ĵ��������Σ������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�

(1) 28cm(2) ��t=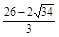 ��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������
��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������
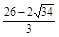 ��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������
��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ����������⣺��1������D��DE��BC�ڵ�E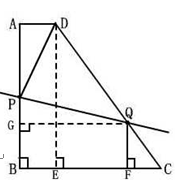
���ı���ABCD��ֱ������
���ı���ABED�Ǿ���
��AD=BE=2��AB=DE=8
��Rt��DEC��CE= =
=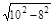 ="6"
="6"
������ABCD���ܳ�= AB+BC+CD+DA=8+8+10+2=28cm.
������3��
��2�� �� ��0��t��8ʱ������Q��QG��AB�ڵ�G
��AP=8��t��DQ=10��t��AD=2��
��Rt��CQF��Rt��CDE
��CF=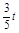 ��QF=
��QF=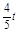 ����PG=
����PG= =
= ��QG=8��
��QG=8��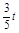
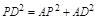 =��8��t��2+22=t2��16t+68��
=��8��t��2+22=t2��16t+68��
PQ2=QG2+PG2=��8��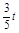 ��2+��
��2+�� ��2=
��2=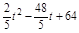
��DQ=PD����10��t��2= t2��16t+68����ã�t=8����������������5��
��DQ=PQ����10��t��2=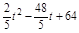 ��
��
��ã�t1=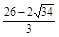 ��t2=
��t2=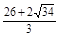 ��8����ȥ������ʱt=
��8����ȥ������ʱt=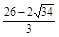 ��������6��
��������6��
�ڵ�8��t��10ʱ��PD=DQ=10��t��
���ʱ��DQΪһ���ĵ�����DPQ������� ����������������7��
�۵�t=10ʱ����P��D��Q�����غϣ������������Σ�������������������8��
�ܵ�10��t��12ʱ��PD="DQ=" t��10��
���ʱ��DQΪһ���ĵ�����DPQ������� ������������������9��
������������t=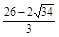 ��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������. ������������������10��
��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������. ������������������10��
��1������D��DE��BC�ڵ�E��Ȼ�����AD=BE=2��AB=DE=8����Rt��DEC�У�����CE=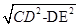 ���CE���������BC�ij����Ӷ��������ABCD���ܳ�
���CE���������BC�ij����Ӷ��������ABCD���ܳ�
��2����i����0��t��8ʱ������Q��QG��AB�ڵ�G������Q��QF��CB�ڵ�F�����ݡ�CQF�ס�CDE�ó�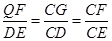 ������CF=
������CF= 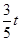 ��QF=
��QF= 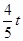 ������PG=t
������PG=t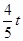 =
= 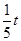 ��QG=8-
��QG=8-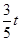 ��Ȼ��ֱ���t��ʾ��PD2=t2-16t+68��PQ2=
��Ȼ��ֱ���t��ʾ��PD2=t2-16t+68��PQ2=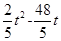 +64����DQ=PD����10-t��2=t2-16t+68����DQ=PQ����10-t��2=
+64����DQ=PD����10-t��2=t2-16t+68����DQ=PQ����10-t��2=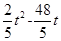 +64�����ⷽ�̼��ɣ�
+64�����ⷽ�̼��ɣ�
��ii����8��t��10ʱ��PD=DQ=10-t����ʱ��DQΪһ���ĵ�����DPQ�����������t=10ʱ����P��D��Q�����غϣ������������Σ���10��t��12ʱ��PD="DQ=" t��10����ʱ��DQΪһ���ĵ�����DPQ��������Ӷ��ó����𰸣�

���ı���ABCD��ֱ������
���ı���ABED�Ǿ���
��AD=BE=2��AB=DE=8
��Rt��DEC��CE=
 =
=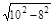 ="6"
="6" ������ABCD���ܳ�= AB+BC+CD+DA=8+8+10+2=28cm.
������3��
��2�� �� ��0��t��8ʱ������Q��QG��AB�ڵ�G
��AP=8��t��DQ=10��t��AD=2��
��Rt��CQF��Rt��CDE
��CF=
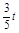 ��QF=
��QF=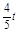 ����PG=
����PG= =
= ��QG=8��
��QG=8��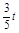
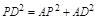 =��8��t��2+22=t2��16t+68��
=��8��t��2+22=t2��16t+68��PQ2=QG2+PG2=��8��
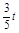 ��2+��
��2+�� ��2=
��2=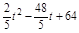
��DQ=PD����10��t��2= t2��16t+68����ã�t=8����������������5��
��DQ=PQ����10��t��2=
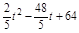 ��
�� ��ã�t1=
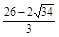 ��t2=
��t2=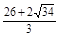 ��8����ȥ������ʱt=
��8����ȥ������ʱt=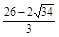 ��������6��
��������6���ڵ�8��t��10ʱ��PD=DQ=10��t��
���ʱ��DQΪһ���ĵ�����DPQ������� ����������������7��
�۵�t=10ʱ����P��D��Q�����غϣ������������Σ�������������������8��
�ܵ�10��t��12ʱ��PD="DQ=" t��10��
���ʱ��DQΪһ���ĵ�����DPQ������� ������������������9��
������������t=
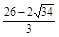 ��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������. ������������������10��
��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������. ������������������10����1������D��DE��BC�ڵ�E��Ȼ�����AD=BE=2��AB=DE=8����Rt��DEC�У�����CE=
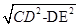 ���CE���������BC�ij����Ӷ��������ABCD���ܳ�
���CE���������BC�ij����Ӷ��������ABCD���ܳ���2����i����0��t��8ʱ������Q��QG��AB�ڵ�G������Q��QF��CB�ڵ�F�����ݡ�CQF�ס�CDE�ó�
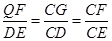 ������CF=
������CF= 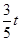 ��QF=
��QF= 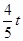 ������PG=t
������PG=t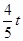 =
= 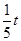 ��QG=8-
��QG=8-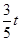 ��Ȼ��ֱ���t��ʾ��PD2=t2-16t+68��PQ2=
��Ȼ��ֱ���t��ʾ��PD2=t2-16t+68��PQ2=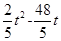 +64����DQ=PD����10-t��2=t2-16t+68����DQ=PQ����10-t��2=
+64����DQ=PD����10-t��2=t2-16t+68����DQ=PQ����10-t��2=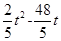 +64�����ⷽ�̼��ɣ�
+64�����ⷽ�̼��ɣ���ii����8��t��10ʱ��PD=DQ=10-t����ʱ��DQΪһ���ĵ�����DPQ�����������t=10ʱ����P��D��Q�����غϣ������������Σ���10��t��12ʱ��PD="DQ=" t��10����ʱ��DQΪһ���ĵ�����DPQ��������Ӷ��ó����𰸣�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
��ͼ������ABCD��DC��AB��AB =2DC���Խ���AC��BD�ཻ���ϣ�BD =4����AC���е�H��EF��BD�ֱ�AB��AD�ڵ�E��F����EF�ij�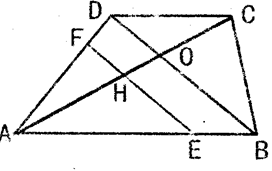


 S�ı���OQPBʱ����ȷ����P��AB�ϵ�λ�ã�������߶�PQ�ij���
S�ı���OQPBʱ����ȷ����P��AB�ϵ�λ�ã�������߶�PQ�ij���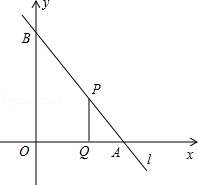

 3��AC=3
3��AC=3 �����O�İ뾶����
�����O�İ뾶����