题目内容
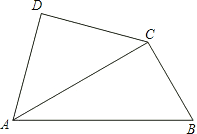
【题目】将一副三角尺如图拼接:含![]() 角的三角尺
角的三角尺![]() 的长直角边与含
的长直角边与含![]() 角的三角尺
角的三角尺![]() 的斜边恰好重合
的斜边恰好重合![]() 已知
已知![]() 是AC上的一个动点.
是AC上的一个动点.
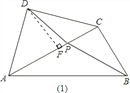
![]() 当点P运动到
当点P运动到![]() 的平分线上时,连接DP,求DP的长;
的平分线上时,连接DP,求DP的长;
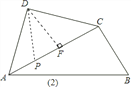
![]() 当点P在运动过程中出现
当点P在运动过程中出现![]() 时,求此时
时,求此时![]() 的度数;
的度数;
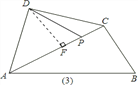
![]() 当点P运动到什么位置时,以
当点P运动到什么位置时,以![]() 为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
【答案】(1)![]() ;(2)
;(2)![]() 的度数为
的度数为![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)、作DF⊥AC,由AB的长求得BC、AC的长.在等腰Rt△DAC中,DF=FA=FC;在Rt△BCP中,求得PC的长.则由勾股定理即可求得DP的长;(2)、由(1)得BC与DF的关系,则DP与DF的关系也已知,先求得∠PDF的度数,则∠PDA的度数也可求出,需注意有两种情况;(3)、由于四边形DPBQ为平行四边形,则BC∥DF,P为AC中点,作出平行四边形,求得面积.
详解:(1)解:在![]() 中,
中,![]() ,
,
![]() .
.
![]() 如图
如图![]() ,作
,作![]() .
.
![]() 中,
中,![]() ,
,![]() .
.![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() 当P点位置如图
当P点位置如图![]() 所示时,根据
所示时,根据![]() 中结论,
中结论,![]() ,
,
又![]() ,
,![]() ,
,![]() .
.
![]() .
.
当P点位置如图![]() 所示时,同
所示时,同![]() 可得
可得![]() .
.
![]() . 故
. 故![]() 的度数为
的度数为![]() 或
或![]() ;
;
![]() 当点P运动到边AC中点
当点P运动到边AC中点![]() 如图
如图![]() ,即
,即![]() 时,
时,
以![]() 为顶点的平行四边形的顶点Q恰好在边BC上.
为顶点的平行四边形的顶点Q恰好在边BC上.
![]() 四边形DPBQ为平行四边形,
四边形DPBQ为平行四边形,![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
而在![]() 中,
中,![]() ,
,![]() 根据勾股定理得:
根据勾股定理得:![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,
![]() 是平行四边形DPBQ的高,
是平行四边形DPBQ的高,![]() .
.


练习册系列答案
相关题目



