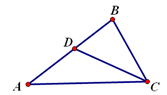
题目内容
如图,一次函数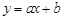 与
与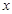 轴,
轴,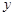 轴交于A,B两点,与反比例函数y=k/x相交于C,D两点,分别过C,D两点作
轴交于A,B两点,与反比例函数y=k/x相交于C,D两点,分别过C,D两点作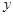 轴,
轴,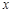 轴的垂线,垂足为E,F,连接CF,DE,EF.有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④
轴的垂线,垂足为E,F,连接CF,DE,EF.有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④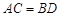 .其中正确的结论个数是( )
.其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
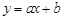 与
与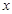 轴,
轴,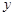 轴交于A,B两点,与反比例函数y=k/x相交于C,D两点,分别过C,D两点作
轴交于A,B两点,与反比例函数y=k/x相交于C,D两点,分别过C,D两点作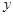 轴,
轴,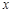 轴的垂线,垂足为E,F,连接CF,DE,EF.有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④
轴的垂线,垂足为E,F,连接CF,DE,EF.有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④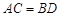 .其中正确的结论个数是( )
.其中正确的结论个数是( ) 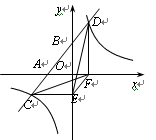 |
A. 1 B. 2 C. 3 D. 4
B
此题要根据反比例函数的性质进行求解,解决此题的关键是要证出CD∥EF,可从①问的面积相等入手;△DFE中,以DF为底,OF为高,可得S△DFE=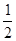
|xD|?|yD|=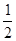 k,同理可求得△CEF的面积也是
k,同理可求得△CEF的面积也是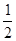 k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
:解:设点D的坐标为(x, ),则F(x,0).
),则F(x,0).
由函数的图象可知:x>0,k>0.
∴S△DFE=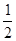 DF?OF=
DF?OF=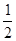 |xD|?|
|xD|?|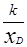 |=
|=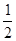 k,
k,
同理可得S△CEF=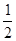 k,
k,
故S△DEF=S△CEF.
若两个三角形以EF为底,则EF边上的高相等,故CD∥EF.
①由上面的解题过程可知:①正确;
②∵CD∥EF,即AB∥EF,∴△AOB∽△FOE,故②正确;
③条件不足,无法得到判定两三角形全等的条件,故③错误;
④法一:∵CD∥EF,DF∥BE,
∴四边形DBEF是平行四边形,
∴S△DEF=S△BED,
同理可得S△ACF=S△ECF;
由①得:S△DBE=S△ACF.
又∵CD∥EF,BD、AC边上的高相等,
∴BD=AC,④正确;
法2:∵四边形ACEF,四边形BDEF都是平行四边形,
而且EF是公共边,
即AC=EF=BD,
∴BD=AC,④正确;
因此正确的结论有3个:①②④.
所以本题选C.
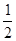
|xD|?|yD|=
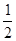 k,同理可求得△CEF的面积也是
k,同理可求得△CEF的面积也是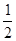 k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.:解:设点D的坐标为(x,
 ),则F(x,0).
),则F(x,0).由函数的图象可知:x>0,k>0.
∴S△DFE=
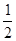 DF?OF=
DF?OF=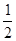 |xD|?|
|xD|?|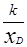 |=
|=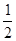 k,
k,同理可得S△CEF=
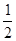 k,
k,故S△DEF=S△CEF.
若两个三角形以EF为底,则EF边上的高相等,故CD∥EF.
①由上面的解题过程可知:①正确;
②∵CD∥EF,即AB∥EF,∴△AOB∽△FOE,故②正确;
③条件不足,无法得到判定两三角形全等的条件,故③错误;
④法一:∵CD∥EF,DF∥BE,
∴四边形DBEF是平行四边形,
∴S△DEF=S△BED,
同理可得S△ACF=S△ECF;
由①得:S△DBE=S△ACF.
又∵CD∥EF,BD、AC边上的高相等,
∴BD=AC,④正确;
法2:∵四边形ACEF,四边形BDEF都是平行四边形,
而且EF是公共边,
即AC=EF=BD,
∴BD=AC,④正确;
因此正确的结论有3个:①②④.
所以本题选C.

练习册系列答案
相关题目
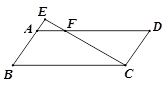
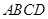 中,点
中,点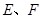 分别在边
分别在边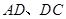 上,
上,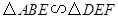 ,AB=6,AE=8,DE=2,求
,AB=6,AE=8,DE=2,求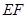 的长.
的长.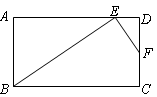
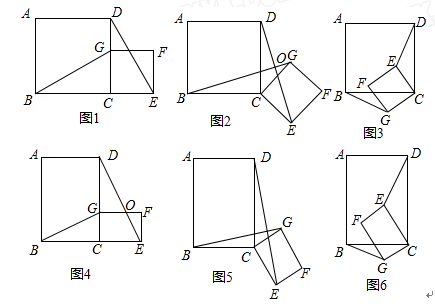
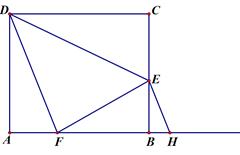
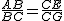 =k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
=k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).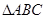 与
与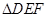 相似,则点F应是甲、乙、丙、丁四点中的( ).
相似,则点F应是甲、乙、丙、丁四点中的( ).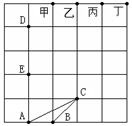

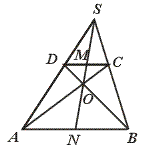
 中,
中, ,且
,且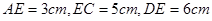 ,则
,则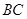 等于( )
等于( )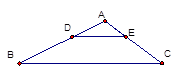

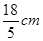
 ,且BD=2,AD=3,求BC的长。
,且BD=2,AD=3,求BC的长。