题目内容
如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,t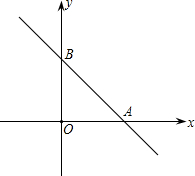 an∠OAB=2.二次函数y=ax2+bx+2的图象经过点A、B,顶点为D,对称轴为x=3
an∠OAB=2.二次函数y=ax2+bx+2的图象经过点A、B,顶点为D,对称轴为x=3
(1)求这个二次函数的解析;
(2)设二次函数y=ax2+bx+2的图象与x轴交另一点C,则二次函数图象上是否存在点P(m,n)(其中1<m<5)使四边形PABC的面积最大?若存在,求出点P的坐标和四边形PABC面积最大值;若不存在,请说明理由;
(3)已知Q为x轴上一点(异与A点),当以Q,B,O三点为顶点的三角形与△OAB相似时,求点Q的坐标.
解:(1)由题意,点B的坐标是(0,2)
∴OB=2
∵tan∠OAB=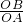 =2,
=2,
∴OA=1,点A(1,0)
∴0=a+b+2,b=-6a;
∴a=0.4,b=-2.4
∴所求解析式是y=0.4x2-2.4x+2;
(2)由(1)题得:顶点D(3,-1.6),点C(5,0)
∴S△ABC=4,
∴当△PAC面积最大时,四边形PABC的面积取最大值;
∵S△PAC不大于S△DAC,
∴当P(3,-1.6)时,四边形PABC的面积取最大值7.2;
(3)当以Q,B,O三点为顶点的三角形与△OAB相似时
需满足: 或
或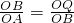
当 时,OQ=OA=1,
时,OQ=OA=1,
∴Q(-1,0)或Q(1,0)(舍去)
当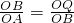 时,OQ=4,
时,OQ=4,
∴Q(-4,0)或Q(4,0)
综上:∴Q(-1,0)或Q(-4,0)或Q(4,0).
分析:(1)根据抛物线的解析式可得出C(0,2),即OB=2,在直角三角形OAB中,根据OB的长和∠OAB的正切值,即可求出OA的长,然后将A点坐标和对称轴解析式代入抛物线中即可求出待定系数的值.
(2)先根据抛物线的解析式求出C点坐标,由于△ABC的面积为定值,因此△PAC的面积最大时,四边形PABC的面积最大,此时P点为抛物线的顶点,据此可求出P的坐标和四边形的面积.
(3)本题要分两种情况进行讨论:
①△QBO∽△ABO,此时两三角形全等,OQ=OA=1,由此可得出Q点的坐标.
②△QBO∽△BAO,可得出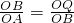 ,由此可求出OQ的长,即可得出Q点的坐标.
,由此可求出OQ的长,即可得出Q点的坐标.
点评:本题考查了二次函数解析式的确定、图形面积的求法、相似三角形的判定和性质等知识点.(3)题在不确定相似三角形的对应角和对应边的情况下要分类进行求解,不要漏解.
∴OB=2
∵tan∠OAB=
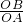 =2,
=2,∴OA=1,点A(1,0)
∴0=a+b+2,b=-6a;
∴a=0.4,b=-2.4
∴所求解析式是y=0.4x2-2.4x+2;
(2)由(1)题得:顶点D(3,-1.6),点C(5,0)
∴S△ABC=4,
∴当△PAC面积最大时,四边形PABC的面积取最大值;
∵S△PAC不大于S△DAC,
∴当P(3,-1.6)时,四边形PABC的面积取最大值7.2;
(3)当以Q,B,O三点为顶点的三角形与△OAB相似时
需满足:
 或
或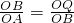
当
 时,OQ=OA=1,
时,OQ=OA=1,∴Q(-1,0)或Q(1,0)(舍去)
当
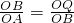 时,OQ=4,
时,OQ=4,∴Q(-4,0)或Q(4,0)
综上:∴Q(-1,0)或Q(-4,0)或Q(4,0).
分析:(1)根据抛物线的解析式可得出C(0,2),即OB=2,在直角三角形OAB中,根据OB的长和∠OAB的正切值,即可求出OA的长,然后将A点坐标和对称轴解析式代入抛物线中即可求出待定系数的值.
(2)先根据抛物线的解析式求出C点坐标,由于△ABC的面积为定值,因此△PAC的面积最大时,四边形PABC的面积最大,此时P点为抛物线的顶点,据此可求出P的坐标和四边形的面积.
(3)本题要分两种情况进行讨论:
①△QBO∽△ABO,此时两三角形全等,OQ=OA=1,由此可得出Q点的坐标.
②△QBO∽△BAO,可得出
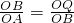 ,由此可求出OQ的长,即可得出Q点的坐标.
,由此可求出OQ的长,即可得出Q点的坐标.点评:本题考查了二次函数解析式的确定、图形面积的求法、相似三角形的判定和性质等知识点.(3)题在不确定相似三角形的对应角和对应边的情况下要分类进行求解,不要漏解.

练习册系列答案
相关题目

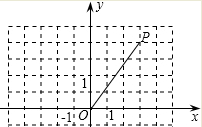 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
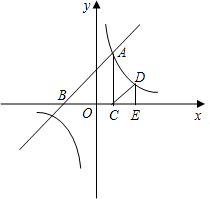
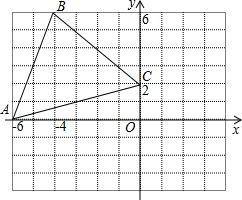 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: