题目内容
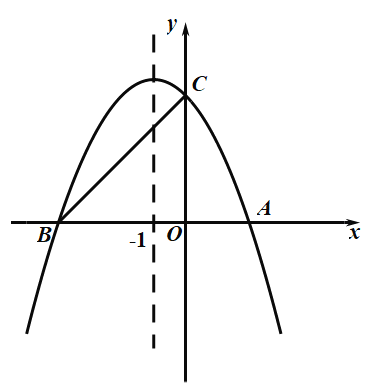
【题目】在平面直角坐标系xOy中,橫、纵坐标都是整数的点叫做整点.直线y=ax与抛物线y=ax2﹣2ax﹣1(a≠0)围成的封闭区域(不包含边界)为W.
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当a=![]() 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围.
【答案】(1)(1,﹣a﹣1);(2)(1,0)、(2,0)、(3,1)、(1,﹣1);(3)区域W内有3个整点,a的取值范围为:a=![]() 或﹣
或﹣![]() ≤a<﹣1
≤a<﹣1
【解析】
(1)将抛物线化成顶点式表达式即可求解;
(2)概略画出直线y=![]() x和抛物线y=
x和抛物线y=![]() x2﹣x﹣1的图象,通过观察图象即可求解;
x2﹣x﹣1的图象,通过观察图象即可求解;
(3)分a>0、a<0两种情况,结合(2)的结论,逐次探究即可求解.
解:(1)y=ax2﹣2ax﹣1=a(x﹣1)2﹣a﹣1,
故顶点的坐标为:(1,﹣a﹣1);
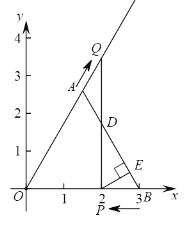
(2)a=![]() 时,概略画出直线y=
时,概略画出直线y=![]() x和抛物线y=
x和抛物线y=![]() x2﹣x﹣1的图象如下:
x2﹣x﹣1的图象如下:
从图中看,W区域整点为如图所示4个黑点的位置,
其坐标为:(1,0)、(2,0)、(3,1)、(1,﹣1);
(3)①当a>0时,
由(2)知,当a=![]() 时,区域W内的所有整点数有4个;
时,区域W内的所有整点数有4个;
参考(2)可得:当a>![]() 时,区域W内的所有整点数多于3个;
时,区域W内的所有整点数多于3个;
当![]() a
a![]() 时,区域W内的所有整点数有4个;
时,区域W内的所有整点数有4个;
同理当a=![]() 时,区域W内的所有整点数有3个;
时,区域W内的所有整点数有3个;
当0<a<![]() 时,区域W内的所有整点数多于3个;
时,区域W内的所有整点数多于3个;
②当a<0时,
当﹣1≤a<0时,区域W内的所有整点数为0个;
当a<﹣![]() 时,区域W内的所有整点数多于3个;
时,区域W内的所有整点数多于3个;
∴区域W内有3个整点时,a的取值范围为:﹣![]() ≤a<﹣1,
≤a<﹣1,
综上,区域W内有3个整点,a的取值范围为:a=![]() 或﹣
或﹣![]() ≤a<﹣1.
≤a<﹣1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目