题目内容
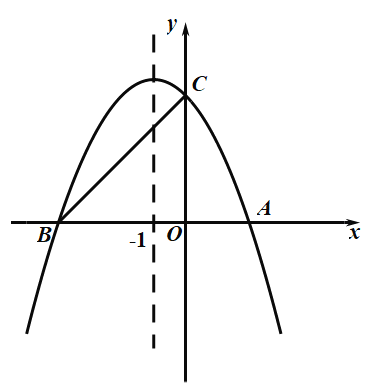
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,它的对称轴是直线
,它的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 为等腰三角形,请求出符合条件的所有点
为等腰三角形,请求出符合条件的所有点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)符合条件的所有点
;(3)符合条件的所有点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求出即可得出结论;
(2)先求出点B坐标,最后用两点间距离公式即可得出结论;
(3)分三种情况,利用等腰三角形的两腰相等建立方程求解即可得出结论解答.
解:(1)根据题意得: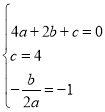 ,
,
解得: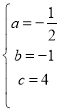 ,
,
∴抛物线的解析式为:![]() ;
;
(2)∵点![]() 的坐标为
的坐标为![]() ,对称轴是直线
,对称轴是直线![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)设![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]()
![]() 是等腰三角形,分三种情况;
是等腰三角形,分三种情况;
①当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() ;
;
②当![]() 时,由(2)知
时,由(2)知![]() ,
,
则![]() ,
,
解得![]() ,
,
∴![]() 或
或![]() ;
;
③当![]() 时,由(2)知
时,由(2)知![]() ,
,
则![]() ,
,
解得![]() 或
或![]() (舍)
(舍)
∴![]() .
.
综上可知,符合条件的所有点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案【题目】下表是小丽在某路口统计![]() 分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊.
分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊.
电瓶车 | 公交车 | 货车 | 小轿车 | 合计(车流总量) | |
(第一时段) |
|
|
| ||
(第二时段) |
|
|
|
| |
合计 |
|
|
(1)根据表格信息,在表格中填写第一时段电瓶车和货车的数量.
(2)在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为![]() 辆.
辆.
①求![]() 的值.
的值.
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加![]() 辆公交车,可减少
辆公交车,可减少![]() 辆小轿车和
辆小轿车和![]() 辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
【题目】为提升英语听力及口语技能,小明打算在手机上安装一款英语口语APP辅助练习.他分别从甲、乙、丙三款口语APP中随机选取了1000条网络评价进行对比,统计如下:
等级 评价数量 APP | 五星 | 四星 | 三星 | 二星 | 一星 | 合计 |
甲 | 562 | 286 | 79 | 48 | 25 | 1000 |
乙 | 517 | 393 | 52 | 21 | 17 | 1000 |
丙 | 504 | 210 | 136 | 116 | 34 | 1000 |
(说明:网上对于口语APP的综合评价从高到低依次为五星、四星、三星、二星和一星).
小明选择________(填“甲”、“乙”或“丙”)款英语口语APP,能获得良好口语辅助练习(即评价不低于四星)的可能性最大.