题目内容
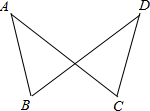 如图,已知AB=DC,DB=AC.求证:∠ABD=∠DCA.
如图,已知AB=DC,DB=AC.求证:∠ABD=∠DCA.分析:连接BC,直接证明△ABC≌△DCB就可以得出∠ABC=∠DCB,∠ACB=∠DBC由等式的性质就可以得出结论.
解答:证明:连接BC,
在△ABC和△DCB中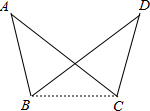
,
∴△ABC≌△DCB(SSS),
∴∠ABC=∠DCB,∠ACB=∠DBC,
∴∠ABC-∠DBC=∠DCB-∠ACB
即∠ABD=∠DCA.
在△ABC和△DCB中

|
∴△ABC≌△DCB(SSS),
∴∠ABC=∠DCB,∠ACB=∠DBC,
∴∠ABC-∠DBC=∠DCB-∠ACB
即∠ABD=∠DCA.
点评:本题考查了全等三角形的判定及性质的而运用,等式的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
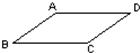 14、如图,已知AB∥DC,要使四边形ABCD是平行四边形,还需增加条件
14、如图,已知AB∥DC,要使四边形ABCD是平行四边形,还需增加条件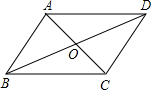 如图,已知AB=DC,AD=BC,那么图中全等三角形的对数是( )
如图,已知AB=DC,AD=BC,那么图中全等三角形的对数是( )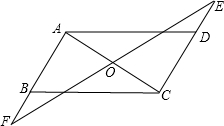 如图,已知AB=DC,AD=CB,过O的直线交AB、CD的延长线于F、E,
如图,已知AB=DC,AD=CB,过O的直线交AB、CD的延长线于F、E,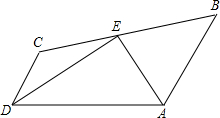 如图:已知AB∥DC,∠BAD和∠ADC的平分线相交于点E,过点E的直线分别交AB、DC于B、C两点.猜想线段AD、AB、DC之间的数量关系,并证明.
如图:已知AB∥DC,∠BAD和∠ADC的平分线相交于点E,过点E的直线分别交AB、DC于B、C两点.猜想线段AD、AB、DC之间的数量关系,并证明.