题目内容
 如图:已知AB∥DC,∠BAD和∠ADC的平分线相交于点E,过点E的直线分别交AB、DC于B、C两点.猜想线段AD、AB、DC之间的数量关系,并证明.
如图:已知AB∥DC,∠BAD和∠ADC的平分线相交于点E,过点E的直线分别交AB、DC于B、C两点.猜想线段AD、AB、DC之间的数量关系,并证明.分析:在AD上截取AF=AB,连接EF,根据SAS证△BAE≌△FAE,推出∠B=∠EFA,求出∠C=∠EFD,证△CDE≌△FDE,推出DC=DF,即可得出答案.
解答: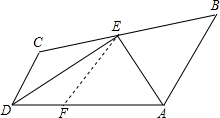
答:AD=AB+DC,
证明:在AD上截取AF=AB,连接EF,
∵AE平分∠BAF,
∴∠BAE=∠FAE,
∵在△BAE和△FAE中
∴△BAE≌△FAE(SAS),
∴∠B=∠EFA,
∵AB∥DC,
∴∠B+∠C=180°,
∵∠EFD+∠EFA=180°,
∴∠C=∠EFD,
∵DE平分∠CDA,
∴∠CDE=∠FDE,
∵在△CDE和△FDE中
∴△CDE≌△FDE(AAS),
∴DC=DF,
∴AD=AF+DF=AB+DC.

答:AD=AB+DC,
证明:在AD上截取AF=AB,连接EF,
∵AE平分∠BAF,
∴∠BAE=∠FAE,
∵在△BAE和△FAE中
|
∴△BAE≌△FAE(SAS),
∴∠B=∠EFA,
∵AB∥DC,
∴∠B+∠C=180°,
∵∠EFD+∠EFA=180°,
∴∠C=∠EFD,
∵DE平分∠CDA,
∴∠CDE=∠FDE,
∵在△CDE和△FDE中
|
∴△CDE≌△FDE(AAS),
∴DC=DF,
∴AD=AF+DF=AB+DC.
点评:本题考查了全等三角形的性质和判定,平行线的性质,角平分线定义等知识点的应用,关键是能正确作辅助线.

练习册系列答案
相关题目
 14、如图,已知AB∥DC,要使四边形ABCD是平行四边形,还需增加条件
14、如图,已知AB∥DC,要使四边形ABCD是平行四边形,还需增加条件 如图,已知AB=DC,AD=BC,那么图中全等三角形的对数是( )
如图,已知AB=DC,AD=BC,那么图中全等三角形的对数是( ) 如图,已知AB=DC,AD=CB,过O的直线交AB、CD的延长线于F、E,
如图,已知AB=DC,AD=CB,过O的直线交AB、CD的延长线于F、E, 如图,已知AB=DC,DB=AC.求证:∠ABD=∠DCA.
如图,已知AB=DC,DB=AC.求证:∠ABD=∠DCA.