题目内容
【题目】如图,在平面直角坐标系中,点C(-4,0),点![]() 分别在
分别在![]() 轴,
轴, ![]() 轴的正半轴上,线段OA、OB的长度都是方程
轴的正半轴上,线段OA、OB的长度都是方程![]() .的解,且OB>OA。若点
.的解,且OB>OA。若点![]() 从
从![]() 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线![]() 运动,连结
运动,连结![]() 。
。
(1)判断三角形ABC的形状
(2)求出![]() 的面积
的面积![]() 关于点
关于点![]() 的运动时间
的运动时间![]() 秒的函数关系式.
秒的函数关系式.
(3)在点P的运动过程中,利用备用图探究,求![]() 周长最短时点P运动的时间。
周长最短时点P运动的时间。

【答案】(1)△ABC为Rt△;
(2)S△PAD= ![]() ;(3)
;(3)![]()
【解析】试题分析:
(1) 观察图形,线段BC、AB、AC与OB的位置关系与射影定理的典型图形相像,容易联想到利用与射影定理相关的条件去判断三角形形状. 解方程易知OA、OB的长度,可以发现OB是OA,OC的比例中项,进而利用相似三角形的判定与性质可以判断△ABC为直角三角形.
(2) 解决三角形面积相关的问题往往需要先确定底和高. 在△AOP中,OA始终不变并且以OA为底的高与y轴平行. 故可以选OA为底,再由点P作出相应的高. 利用高与坐标轴的平行关系,可以通过相似三角形确定所求的函数关系.
(3) 周长最短问题实际是线段之和最短问题. 由题意可知,应该作点A关于直线CB的对称点A',连接OA',当点P为OA'与CB的交点时,三角形周长最小. 由于题目中要求研究该过程,所以需要在解答时较为详细地说明上述最小的原因. 求解当点P为OA'与CB的交点时点P的运动时间,先求解点P的坐标. 由于点P为交点,可以联立直线OA'与CB的方程进行求解. 直线CB的方程易得,直线OA'的方程需要点A'的坐标. 由于点A与点A'关于直线CB对称,可以利用相似三角形解出点A'的坐标. 得到点P的坐标后可以借助第(2)问中的关系将运动时间求出.
试题解析:
(1) △ABC为直角三角形. 理由如下:
∵OA、OB的长度是方程x2-3x+2=0的解,且OB>OA,
又∵x2-3x+2=0的两个解为:x1=2,x2=1,
∴OB=2,OA=1,
∵点C的坐标为(-4, 0),
∴OC=4,
∵OB2=4,OAOC=![]() =4,
=4,
∴OB2= OAOC,即![]() ,
,
∵在△AOB与△BOC中:
![]() ,∠AOB=∠BOC=90°,
,∠AOB=∠BOC=90°,
∴△AOB∽△BOC,
∴∠ABO=∠BCO,∠OAB=∠OBC,
∵在Rt△AOB中,∠ABO+∠OAB=90°,
∴∠ABC=∠ABO+∠OBC=∠ABO+∠OAB=90°,
∴△ABC为直角三角形.
(2) 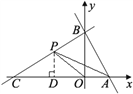
过点P作PD⊥AC,垂足为D. (如图)
∵PD⊥AC,OB⊥AC,
∴PD∥OB,
∴△CPD∽△CBO,
∴![]() ,
,
∵点P从C点出发,以每秒1个单位的速度沿射线CB运动,且点P运动时间为t,
∴CP=1t=t,
∵OB=2,OC=4,
∴在Rt△BOC中, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OA=1,
∴△AOP的面积![]() .
.
(3) 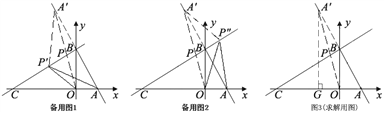
延长线段AB至点A',使得AB=A'B,连接OA',交直线CB于点P.
下面说明当点P为OA'与CB的交点时△AOP的周长最小.
①当点P (图中实际表示该动点的是点P') 在线段CB上运动时(如备用图1),
连接A'P',
∵AB=A'B,∠ABC=90°,
∴直线CB垂直平分线段AA',
∴AP'=A'P',
∵△AOP'的周长为:OA+OP'+AP',
又∵OA=1,
∴△AOP'的周长为:1+OP'+AP'=1+OP'+A'P',
∴当OP'+A'P'取最小值时,△AOP'的周长最小.
∵当点P'不与点P重合时,线段OP',A'P',OA'构成△OP'A',即OP'+A'P'>OA',
又∵当点P'与点P重合时,OP'+A'P'=OA',
∴当点P'与点P重合时,OP'+A'P'最小,即△AOP'的周长最小,
∴当点P在线段CB上运动时,若点P为OA'与CB的交点,则△AOP的周长最小.
②当点P (图中实际表示该动点的是点P") 在线段CB延长线上运动时(如备用图2),
连接A'P",
与①同理可得:AP"=A'P",
又∵△AOP"的周长为:OA+OP"+AP",
与①同理可得:当OP"+A'P"取最小值时,△AOP"的周长最小,
∵当点P"在线段CB延长线上运动时,线段OP",A'P",OA'构成△OP"A',即OP"+A'P">OA',
∴当点P在线段CB延长线上运动时,△AOP的周长均大于当点P为OA'与CB交点时的△AOP的周长.
综上所述,当点P为OA'与CB交点时,△AOP的周长最小.
下面求解当点P为OA'与CB交点时点P的运动时间t.
过点A'作A'G⊥AC,垂足为G,(如图3)
∵A'G⊥AC,
∴A'G∥OB,
∴△AGA'∽△AOB
∴![]() ,
, ![]()
∵AB=A'B,BO=2,AO=1,
∴![]() ,
, ![]() ,
,
∴A'G=4,AG=2,
∴OG=AG-AO=2-1=1,
∴点A'的坐标为(-1,4),
∴直线OA'的方程为:y=-4x,
∵点B的坐标为(0,2),点C的坐标为(-4,0),
∴直线BC的方程为: ![]() ,
,
∵点P为OA'与CB的交点,
∴联立直线OA'与BC的方程:
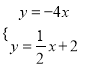 ,
,
解之,得: 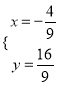 ,
,
即当点P的坐标为![]() 时,△AOP的周长最小.
时,△AOP的周长最小.
由第(2)问的结论知,△AOP的面积![]() ,
,
∵当点P的坐标为![]() 时,△AOP的面积
时,△AOP的面积![]() ,
,
∴![]() (秒),
(秒),
即△AOP的周长最短时点P运动的时间为![]() 秒.
秒.