��Ŀ����
����Ŀ��ʵ����̽��
(1)��ͼ�٣�ͼ�ڣ�ͼ���У�����ƽ���ı���ABCD�Ķ���A��B��D�����꣬д��ͼ�٣�ͼ�ڣ�ͼ���еĶ���C�����꣬���Ƿֱ���________��___________��____________��
(2)��ͼ���У�����ƽ���ı���ABCD�Ķ���A��B��D������(��ͼ��ʾ)���������C������(C�������ú�a��b��c��d��e��f�Ĵ���ʽ��ʾ)��
�����뷢��
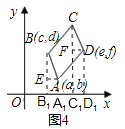
(3)ͨ����ͼ�٣�ͼ�ڣ�ͼ�ۣ�ͼ�ܵĹ۲�Ͷ���C�������̽������ᷢ�֣�����ƽ���ı���ABCD����ֱ������ϵ���ĸ�λ�ã����䶥��C����Ϊ(m��n)(��ͼ��)ʱ�����ĸ�����ĺ�����a��c��m��e֮��ĵ�����ϵΪ___________��������b��d��n��f֮��ĵ�����ϵΪ__________��(����֤��)
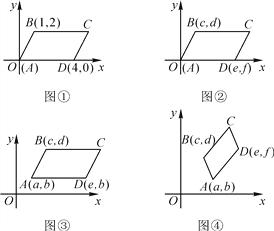
���𰸡�(1) (5��2)��(e��c��d)��(c��e��a��d) ��(2) C(e��c��a��f��d��b) ��(3) m��a��c��e��n��b��d��f
�������������������1������ƽ���ı��ε����ʣ��Ա�ƽ������ȣ��ó�ͼ2��3�ж���C������ֱ��ǣ�e+c��d������c+e��a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1���ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F����ƽ���ı���ABCD�У�CD=BA�������ڽǺͶ���������BB1��CC1�����Ƴ���EBA=��FCD����BEA�ա�CFD��������ó�AF=DF=a��c��BE=CF=d��b����C��x��y������e��x=a��c����x=e+c��a����y��f=d��b����y=f+d��b���̶��Ƴ���C�����꣮
��3����ƽ���ı���ABCD�У�CD=BA��ͬ��֤����BEA�ա�CFD��ͬ��2��֤������Ȼ���Ƴ�AF=DF=a��c��BE=CF=d��b������֪C�������Ϊ��m��n����e��m=a��c����m=e+c��a����n��f=d��b���ó�n=f+d��b��
����������⣺��1������ƽ���ı��ε����ʣ��Ա�ƽ������ȣ��ó�ͼ1��ͼ2��3�ж���C������ֱ��ǣ���5��2������e+c��d������c+e��a��d����
�ʴ�Ϊ����5��2������e+c��d������c+e��a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA1��B1��C1��D1���ֱ��A��D��AE��BB1��E��DF��CC1�ڵ�F��
��ƽ���ı���ABCD�У�CD=BA������BB1��CC1�����EBA+��ABC+��BCF=��ABC+��BCF+��FCD=180�ȣ����EBA=��FCD��
����BEA����CFD�У��ߡ�AEB=��DFC����EFA=��FCD��AB=DC�����BEA�ա�CFD��AAS������AE=DF=a��c��BE=CF=d��b��
��C��x��y������e��x=a��c������x=e+c��a��
��y��f=d��b������y=f+d��b����C��e+c��a��f+d��b����
��3����ƽ���ı���ABCD�У�CD=BA��ͬ���ɵ���BEA�ա�CFD����AF=DF=a��c��BE=CF=d��b����C�������Ϊ��m��n����e��m=a��c����m=e+c��a����n��f=d��b������n=f+d��b���ʴ�Ϊ��m=c+e��a��n=d+f��b��m+a=c+e��n+b=d+f��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�


