题目内容
 如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为________.
如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为________.
32π
分析:根据题意得出小圆扫过的阴影部分的面积等于两个同心圆组成的圆环的面积,两圆的半径分别是9、7(9-1-1=7),根据圆的面积公式求出即可.
解答:根据图形得:小圆扫过的阴影部分的面积是π×92-π×(9-1-1)2=32π,
故答案为32π.
点评:本题考查了相切两圆的性质的应用,主要考查学生的观察图形的能力,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键.
分析:根据题意得出小圆扫过的阴影部分的面积等于两个同心圆组成的圆环的面积,两圆的半径分别是9、7(9-1-1=7),根据圆的面积公式求出即可.
解答:根据图形得:小圆扫过的阴影部分的面积是π×92-π×(9-1-1)2=32π,
故答案为32π.
点评:本题考查了相切两圆的性质的应用,主要考查学生的观察图形的能力,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(2011•潍坊)如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为( )
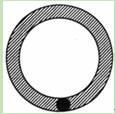

| A.17π | B.32π |
| C.49π | D.80π |
(2011•潍坊)如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为( )
| A.17π | B.32π |
| C.49π | D.80π |
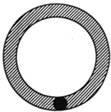 9、如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为( )
9、如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为( )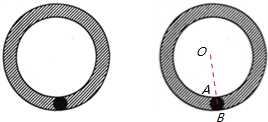 如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为
如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为 如图,半径为r的小圆在半径为R的大圆内.已知阴影部分面积是小圆面积的3倍.则
如图,半径为r的小圆在半径为R的大圆内.已知阴影部分面积是小圆面积的3倍.则