��Ŀ����
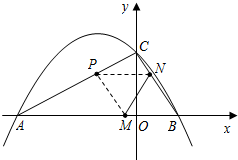 ��ͼ��������y=ax2+bx+c��a��0����x�ύ��A��-3��0����B���㣬��y���ཻ�ڵ�C��0��
��ͼ��������y=ax2+bx+c��a��0����x�ύ��A��-3��0����B���㣬��y���ཻ�ڵ�C��0��| 3 |
��1���������ߵĽ���ʽ��
��2������M��Nʱ��B�����������ÿ��1����λ���ȵ��ٶȷֱ���BA��BC���˶�������һ���㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt��ʱ������MN������BMN��MN���ۣ�B��ǡ������AC���ϵ�P������t��ֵ����P�����ꣻ
��3�������߶Գ������Ƿ����һ��F��ʹ�á�ACF�ǵ��������Σ�����������˵�����ɣ������ڣ������F�����꣮
��������1�����ݵ�x=-4��x=2ʱ�����κ���y=ax2+bx+c��a��0���ĺ���ֵy��ȣ�������ú����ĶԳ��ᣬ����A��B�Գƣ��������B�����꣬Ȼ�����ô���ϵ����������ú����Ľ���ʽ��
��2������M��N����˶��ٶ���ͬ�����Եõ�BM=BN���������ݷ��۵�����֤�����ı���BMPN�����Σ����CPN�����ڡ�CAB���������������ε����ʣ����OD��PD�ij��ȣ���������P�����ꣻ
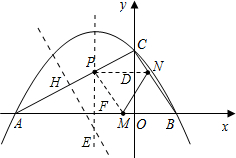
��3����F�ڶԳ����ϣ���F�ĺ�����һ����-1����ACF�ǵ��������Σ���AF=AC��CF=CA��EA=EC��������������ۣ�ǰ�����������t��ʾ��AE��CE�ij��ȣ����ɵõ�����t�ķ��̴Ӷ���⣻������������ֱ��HF�Ľ���ʽ���ٸ���F�ĺ�������-1��������⣮
��2������M��N����˶��ٶ���ͬ�����Եõ�BM=BN���������ݷ��۵�����֤�����ı���BMPN�����Σ����CPN�����ڡ�CAB���������������ε����ʣ����OD��PD�ij��ȣ���������P�����ꣻ
��3����F�ڶԳ����ϣ���F�ĺ�����һ����-1����ACF�ǵ��������Σ���AF=AC��CF=CA��EA=EC��������������ۣ�ǰ�����������t��ʾ��AE��CE�ij��ȣ����ɵõ�����t�ķ��̴Ӷ���⣻������������ֱ��HF�Ľ���ʽ���ٸ���F�ĺ�������-1��������⣮
��� �⣺��1��������ɵã��Գ���Ϊx=
�⣺��1��������ɵã��Գ���Ϊx=
=-1��
�ɶԳ��Կɵ�B������Ϊ��1��0��
���������ߵĽ���ʽΪy=a��x+3����x-1����
�ֹ��� C��0��
��������ɽ��a=-
�����ʽΪy=-
(x+3)(x-1)��
��y=-
x2-
x+
��2����M��N����˶��ٶ���ͬ����BM=BN=t��
���ɷ��ۿɵã�NB=NP=t��MB=MP=t
���ı���BMPN�����Σ���PNƽ��MN����x�ᣩ
���CPN�����ڡ�CAB��
��
=
��AB=4��BC=2
��
=
���t=
��NB=
����CN=
��
=
=
��
����ɽ��CD=
��DN=
��OD=
��PD=1
��P(-1��
)
��3����ֱ�ǡ�AOC�У�AC=
=
=2
��
��F��������1��a��
�ٵ�AF=ACʱ����AC=2
����AE=
=2
��ã�a=��2
��F��-1��2
����-1��-2
����
�ڵ�CF=CAʱ����CE=
=2
��ã�a=
��
��
��F�������ǣ�-1��
+
����-1��
-
����
�۵�EA=ECʱ��E��ΪAC��ֱƽ������Գ���Ľ��㣬�е�H�������ǣ�-
��
����
��ֱ��AC�Ľ���ʽ�ǣ�y=kx+b����������ã�
����ã�
��
��AC�Ľ���ʽ�ǣ�y=
x+
��
��F��ΪAC��ֱƽ������Գ���Ľ��㣬
��ֱ��HF��һ����ϵ����-
��
��HF�Ľ���ʽ��y=-
x+c����H���������ã�-
����-
��+c=
����ã�c=-
��
��HF�Ľ���ʽ�ǣ�y=-
x-
��
��x=-1�����y=0��
��F�������ǣ�-1��0����
��֮��F�������ǣ���-1��2
����-1��-2
����-1��
+
����-1��
-
����-1��0����
 �⣺��1��������ɵã��Գ���Ϊx=
�⣺��1��������ɵã��Գ���Ϊx=| -4+2 |
| 2 |
�ɶԳ��Կɵ�B������Ϊ��1��0��
���������ߵĽ���ʽΪy=a��x+3����x-1����
�ֹ��� C��0��
| 3 |
| ||
| 3 |
�����ʽΪy=-
| ||
| 3 |
��y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
��2����M��N����˶��ٶ���ͬ����BM=BN=t��
���ɷ��ۿɵã�NB=NP=t��MB=MP=t
���ı���BMPN�����Σ���PNƽ��MN����x�ᣩ
���CPN�����ڡ�CAB��
��
| PN |
| AB |
| CN |
| CB |
��
| t |
| 4 |
| 2-t |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
��
| CN |
| CB |
| CD |
| CO |
| DN |
| OB |
����ɽ��CD=
| ||
| 3 |
| 1 |
| 3 |
��OD=
2
| ||
| 3 |
��P(-1��
2
| ||
| 3 |
��3����ֱ�ǡ�AOC�У�AC=
| OA2+OC2 |
| 9+3 |
| 3 |
��F��������1��a��
�ٵ�AF=ACʱ����AC=2
| 3 |
| (-1+3)2+a2 |
| 3 |
��ã�a=��2
| 2 |
��F��-1��2
| 2 |
| 2 |
�ڵ�CF=CAʱ����CE=
12+(a-
|
| 3 |
��ã�a=
| 3 |
| 11 |
��F�������ǣ�-1��
| 3 |
| 11 |
| 3 |
| 11 |
�۵�EA=ECʱ��E��ΪAC��ֱƽ������Գ���Ľ��㣬�е�H�������ǣ�-
| 3 |
| 2 |
| ||
| 2 |
��ֱ��AC�Ľ���ʽ�ǣ�y=kx+b����������ã�
|
|
��AC�Ľ���ʽ�ǣ�y=
| ||
| 3 |
| 3 |
��F��ΪAC��ֱƽ������Գ���Ľ��㣬
��ֱ��HF��һ����ϵ����-
| 3 |
��HF�Ľ���ʽ��y=-
| 3 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
��HF�Ľ���ʽ�ǣ�y=-
| 3 |
| 3 |
��x=-1�����y=0��
��F�������ǣ�-1��0����
��֮��F�������ǣ���-1��2
| 2 |
| 2 |
| 3 |
| 11 |
| 3 |
| 11 |
�����������ǿ����˶��κ��������ε��ж������ʣ�����ϵ���������Ľ���ʽ���ۺ�Ӧ�ã���ȷ֤���ı���BMPN�������ǹؼ���

��ϰ��ϵ�д�
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
�����Ŀ
 ���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣�
���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣� OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1��
OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��x�ύ�ڵ�A��B����A������Ϊ��-2��0����
��x�ύ�ڵ�A��B����A������Ϊ��-2��0����