题目内容
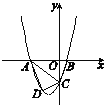
【题目】如图,![]() 为圆
为圆![]() 的直径,
的直径,![]() 为圆
为圆![]() 上一点,
上一点,![]() 为
为![]() 延长线一点,且
延长线一点,且![]() ,
,![]() 于点
于点![]() .
.
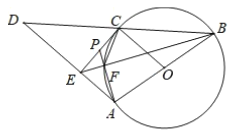
(1)求证:直线![]() 为圆
为圆![]() 的切线;
的切线;
(2)设![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,
,
①求证:![]()
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)说明OC是△BDA的中位线,利用中位线的性质,得到∠OCE=∠CED=90°,从而得到CE是圆O的切线.
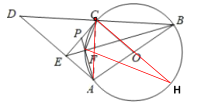
(2)①过点![]() 作直径
作直径![]() ,连接
,连接![]() ,
,![]() ,运用已知条件证明
,运用已知条件证明![]() ,即可得到
,即可得到![]() ,即
,即![]() .
.
②利用直径上的圆周角,得到△PEF是直角三角形,利用角相等,可得到△PEF∽△PEA、△PCF∽△PAC,从而得到PC=PE=5.然后求出sin∠PEF的值
(1)证明:∵![]() 于点
于点![]() ∴
∴![]() ,
,
∵![]() ,∴
,∴![]() 是
是![]() 的中点,又∵
的中点,又∵![]() 是
是![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,∴
,∴![]()
∴![]() ,又∵点
,又∵点![]() 在圆上,
在圆上,
∴![]() 是圆
是圆![]() 的切线.
的切线.
(2)①证明:过点![]() 作直径
作直径![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() 是直径,∴
是直径,∴![]() ∴
∴![]()
∵![]() 是圆
是圆![]() 的切线,∴
的切线,∴![]() ,
,
∴![]() ∴
∴![]()
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]() ∴
∴![]() .
.
②∵直径![]() ,∴
,∴![]() 即
即![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
在![]() 中
中![]() .
.


练习册系列答案
相关题目
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?