题目内容
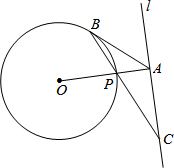 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O 上一点,连接BP并延长,交直线l于点C,使得AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O 上一点,连接BP并延长,交直线l于点C,使得AB=AC.(1)求证:AB是⊙O的切线;
(2)若PC=2
| 5 |
考点:切线的判定
专题:
分析:(1)连接OB,根据等腰三角形性质得出∠ABC=∠ACB,∠OBP=∠OPB,求出∠ABC+∠OBP=90°,根据切线的判定推出即可.
(2)延长AO交⊙O于D,连接BD,设⊙O半径为R,则AP=5-R,OB=R,根据勾股定理得出方程52-R2=(2
)2-(5-R)2,求出R即可.求出AC=AB=4,△DBP∽△CAP,得出
=
,代入求出BP即可.
(2)延长AO交⊙O于D,连接BD,设⊙O半径为R,则AP=5-R,OB=R,根据勾股定理得出方程52-R2=(2
| 5 |
| CP |
| PD |
| AP |
| BP |
解答:(1)证明:
连接OB,
∵OA⊥直线l,
∴∠PAC=90°,
∴∠APC+∠ACP=90°,
∵AB=AC,OB=OP,
∴∠ABC=∠ACB,∠OBP=∠OPB,
∵∠BPO=∠APC,
∴∠ABC+∠OBP=90°,
∴OB⊥AB,
∵OB过O,
∴AB是⊙O的切线;
(2)解:
延长AO交⊙O于D,连接BD,
设⊙O半径为R,则AP=5-R,OB=R,
在Rt△OBA中,AB2=52-R2,在Rt△APC中,AC2=(2
)2-(5-R)2,
∵AB=AC,
∴52-R2=(2
)2-(5-R)2,
解得:R=3,
即⊙O半径为3,
则AC=AB=4,
∵PD为直径,OA⊥直线l,
∴∠DBP=∠PAC,
∵∠APC=∠BPD,
∴△DBP∽△CAP,
∴
=
,
∴
=
,
∴PB=
.

连接OB,
∵OA⊥直线l,
∴∠PAC=90°,
∴∠APC+∠ACP=90°,
∵AB=AC,OB=OP,
∴∠ABC=∠ACB,∠OBP=∠OPB,
∵∠BPO=∠APC,
∴∠ABC+∠OBP=90°,
∴OB⊥AB,
∵OB过O,
∴AB是⊙O的切线;
(2)解:

延长AO交⊙O于D,连接BD,
设⊙O半径为R,则AP=5-R,OB=R,
在Rt△OBA中,AB2=52-R2,在Rt△APC中,AC2=(2
| 5 |
∵AB=AC,
∴52-R2=(2
| 5 |
解得:R=3,
即⊙O半径为3,
则AC=AB=4,
∵PD为直径,OA⊥直线l,
∴∠DBP=∠PAC,
∵∠APC=∠BPD,
∴△DBP∽△CAP,
∴
| CP |
| PD |
| AP |
| BP |
∴
2
| ||
| 6 |
| 2 |
| BP |
∴PB=
6
| ||
| 5 |
点评:本题考查了切线的判定,等腰三角形的性质,相似三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数
已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数 在平面直角坐标系xOy中,A点的坐标为(3,4),将OA绕原点O顺时针旋转90°得到OA′,求点A′的坐标.
在平面直角坐标系xOy中,A点的坐标为(3,4),将OA绕原点O顺时针旋转90°得到OA′,求点A′的坐标. 如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.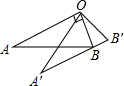 如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanA=
如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanA= 如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为( )
如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为( )