题目内容
 如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.(1)点D在线段PQ上,且DQ=DC.求证:CD是⊙O的切线;
(2)若sinQ=
| 3 |
| 5 |
考点:切线的判定
专题:
分析:1)连结OC,由OC=OB得∠2=∠B,DQ=DC得∠1=∠Q,根据QP⊥PB得到∠Q+∠B=90°,则∠1+∠2=90°,再利用平角的定义得到∠DCO=90°,然后根据切线的判定定理得到CD为⊙O的切线;
(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据余弦的定义得cosB=
=
=
,可计算出BC=
,在Rt△BPQ中,利用余弦的定义得cosB=
=
,可计算出BQ=10,然后利用QC=BQ-BC进行计算即可.
(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据余弦的定义得cosB=
| BC |
| AB |
| BC |
| AP+PB |
| 3 |
| 5 |
| 21 |
| 5 |
| PB |
| BQ |
| 3 |
| 5 |
解答:证明:(1)连结OC,如图,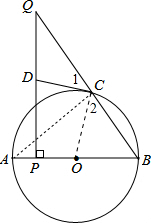
∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°-∠1-∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)解:连接AC,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,cosB=
=
=
,
而BP=6,AP=1,
∴BC=
,
在Rt△BPQ中,cosB=
=
,
∴BQ=
=10,
∴QC=BQ-BC=10-
=
.

∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°-∠1-∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)解:连接AC,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,cosB=
| BC |
| AB |
| BC |
| AP+PB |
| 3 |
| 5 |
而BP=6,AP=1,
∴BC=
| 21 |
| 5 |
在Rt△BPQ中,cosB=
| PB |
| BQ |
| 3 |
| 5 |
∴BQ=
| 6 | ||
|
∴QC=BQ-BC=10-
| 21 |
| 5 |
| 29 |
| 5 |
点评:本题考查了切线的判定和解直角三角形的应用,切线的判定定理是:过半径的外端点与半径垂直的直线为圆的切线.也考查圆周角定理的推论以及解直角三角形.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
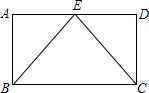 如图,长方形ABCD中,BE、CE分别平分∠ABC和∠DCB,点E在AD上,
如图,长方形ABCD中,BE、CE分别平分∠ABC和∠DCB,点E在AD上,①△ABE≌△DCE;②△ABE和△DCE都是等腰直角三角形;③AE=DE;④△BCE是等边三角形,
以上结论正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数y=
已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数y=| k |
| x |
(1)求点A的坐标及k的值;
(2)试在x轴上确定一点B,使CB=CA,求出点B的坐标.
 如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是( )| A、40° | B、50° |
| C、60° | D、80° |
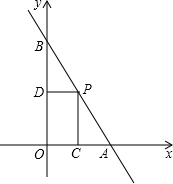 如图,直线y=-2x+8交x轴于A,交Y轴于B,点P在线段AB上,过点P分别向x轴、y轴引垂线,垂足为C、D,设点P的横坐标为m,矩形PCOD的面积为S.
如图,直线y=-2x+8交x轴于A,交Y轴于B,点P在线段AB上,过点P分别向x轴、y轴引垂线,垂足为C、D,设点P的横坐标为m,矩形PCOD的面积为S. 在平面直角坐标系xOy中,A点的坐标为(3,4),将OA绕原点O顺时针旋转90°得到OA′,求点A′的坐标.
在平面直角坐标系xOy中,A点的坐标为(3,4),将OA绕原点O顺时针旋转90°得到OA′,求点A′的坐标.