题目内容
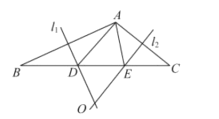
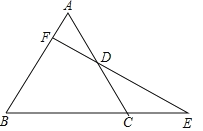
【题目】如图,△ABC是等边三角形,延长BC到E,使CE=![]() BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
(1)EF⊥AB;(2)DE=2DF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等边三角形的性质得出AC=BC,∠ACB=∠B=60°,求出CD=CE,根据三角形外角性质和等腰三角形的性质求出∠E=30°,求出∠BFE即可;
(2)连接BD,求出BD=DE,根据含30°角的直角三角形的性质得出BD=2DF,即可得出答案.
证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵D为AC的中点,
∴AD=CD=![]() AC,
AC,
∵CE=![]() BC,
BC,
∴CD=CE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,
即EF⊥AB;
(2)连接BD,

∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,
∴BD=2DF,
即DE=2DF.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目