ЬтФПФкШн
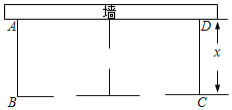
ЁОЬтФПЁПФГХЉГЁвЊНЈвЛИіЫЧбјГЁЃЈГЄЗНаЮ![]() ЃЌЫЧбјГЁЕФвЛУцППЧНЃЈЧНзюДѓПЩгУГЄЖШЮЊ27УзЃЉЃЌСэШ§БпгУФОРИЮЇГЩЃЌжаМфвВгУФОРИИєПЊЃЌЗжГЩСНИіГЁЕиЃЌВЂдкШчЭМЫљЪОЕФШ§ДІИїСє1УзПэЕФУХЃЈВЛгУФОРИЃЉЃЌНЈГЩКѓФОРИзмГЄ60УзЃЌЩшЫЧбјГЁЃЈГЄЗНаЮ
ЃЌЫЧбјГЁЕФвЛУцППЧНЃЈЧНзюДѓПЩгУГЄЖШЮЊ27УзЃЉЃЌСэШ§БпгУФОРИЮЇГЩЃЌжаМфвВгУФОРИИєПЊЃЌЗжГЩСНИіГЁЕиЃЌВЂдкШчЭМЫљЪОЕФШ§ДІИїСє1УзПэЕФУХЃЈВЛгУФОРИЃЉЃЌНЈГЩКѓФОРИзмГЄ60УзЃЌЩшЫЧбјГЁЃЈГЄЗНаЮ![]() ЕФПэЮЊ
ЕФПэЮЊ![]() УзЃЎ
УзЃЎ
ЃЈ1ЃЉЧѓЫЧбјГЁЕФГЄ![]() ЃЈгУКЌ
ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЃЈ2ЃЉШєЫЧбјГЁЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌЫЧбјГЁЕФУцЛ§зюДѓЃЌДЫЪБЫЧбјГЁДяЕНЕФзюДѓУцЛ§ЮЊЖрЩй
ЮЊКЮжЕЪБЃЌЫЧбјГЁЕФУцЛ§зюДѓЃЌДЫЪБЫЧбјГЁДяЕНЕФзюДѓУцЛ§ЮЊЖрЩй![]() ЃП
ЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() УзЃЛЃЈ2ЃЉ15ЃЛЃЈ3ЃЉЕБ
УзЃЛЃЈ2ЃЉ15ЃЛЃЈ3ЃЉЕБ![]() ЮЊ12ЪБЃЌЫЧбјГЁЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЮЊ
ЮЊ12ЪБЃЌЫЧбјГЁЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтКЭЭМаЮЃЌПЩвдгУКЌ![]() ЕФДњЪ§ЪНБэЪОГі
ЕФДњЪ§ЪНБэЪОГі![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉИљОнГЄЗНаЮЕФУцЛ§МЦЫуЙЋЪНПЩвдЕУЕНЯргІЕФЗНГЬЃЌДгЖјПЩвдЕУЕН![]() ЕФжЕЃЌзЂвтЧНзюДѓПЩгУГЄЖШЮЊ27УзЃЛ
ЕФжЕЃЌзЂвтЧНзюДѓПЩгУГЄЖШЮЊ27УзЃЛ
ЃЈ3ЃЉИљОнЬтвтПЩвдЕУЕН![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪКЭ
ЕФКЏЪ§ЙиЯЕЪНЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪКЭ![]() ЕФШЁжЕЗЖЮЇЃЌНтД№МДПЩЃЎ
ЕФШЁжЕЗЖЮЇЃЌНтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉгЩЭМПЩЕУЃЌ![]() ЕФГЄЪЧ
ЕФГЄЪЧ![]() ЃЈУз
ЃЈУз![]() ЃЌ
ЃЌ
МД![]() ЕФГЄЪЧ
ЕФГЄЪЧ![]() УзЃЛ
УзЃЛ
ЃЈ2ЃЉСю![]() ЃЌНтЕУЃЌ
ЃЌНтЕУЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
МД![]() ЕФжЕЪЧ15ЃЛ
ЕФжЕЪЧ15ЃЛ
ЃЈ3ЃЉЩшЫЧбјГЁЕФУцЛ§ЪЧ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕЃЌДЫЪБ
ШЁЕУзюДѓжЕЃЌДЫЪБ![]() ЃЌ
ЃЌ
Д№ЃКЕБ![]() ЮЊ12ЪБЃЌЫЧбјГЁЕФУцЛ§зюДѓЃЌДЫЪБЫЧбјГЁДяЕНЕФзюДѓУцЛ§ЮЊ
ЮЊ12ЪБЃЌЫЧбјГЁЕФУцЛ§зюДѓЃЌДЫЪБЫЧбјГЁДяЕНЕФзюДѓУцЛ§ЮЊ![]() ЃЎ
ЃЎ

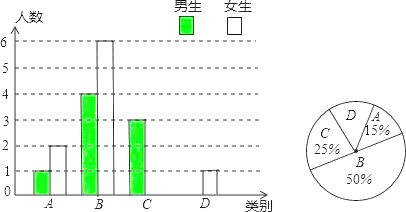
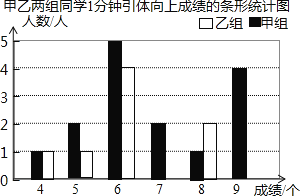
ЁОЬтФПЁПМзЁЂввСНзщЭЌбЇНјаавЛЗжжгв§ЬхЯђЩЯВтЪдЃЌЦРЗжБъзМЙцЖЈЃЌзі6ИівдЩЯ![]() КЌ6Иі
КЌ6Иі![]() ЮЊКЯИёЃЌзі9ИівдЩЯ
ЮЊКЯИёЃЌзі9ИівдЩЯ![]() КЌ9Иі
КЌ9Иі![]() ЮЊгХауЃЌСНзщЭЌбЇЕФВтЪдГЩМЈШчЯТБэЃК
ЮЊгХауЃЌСНзщЭЌбЇЕФВтЪдГЩМЈШчЯТБэЃК
ГЩМЈ | ЁЁ4 | ЁЁ5 | ЁЁ6 | ЁЁ7 | ЁЁ8 | ЁЁ9 |
ЁЁМззщ | ЁЁ1 | ЁЁ2 | ЁЁ5 | ЁЁ2 | ЁЁ1 | ЁЁ4 |
ЁЁввзщ | ЁЁ1 | ЁЁ1 | ЁЁ4 | ЁЁ5 | ЁЁ2 | ЁЁ2 |
ЯжНЋСНзщЭЌбЇЕФВтЪдГЩМЈЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМБэЃК
ЭГМЦСП | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | ЗНВю | КЯИёТЪ | гХауТЪ |
Мззщ | a | 6 | 6 |
|
|
|
ввзщ |
| b | 7 |
|
|
|
![]() НЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
НЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
![]() ЭГМЦБэжаЕФ
ЭГМЦБэжаЕФ![]() ______ЃЌ
______ЃЌ![]() ______ЃЛ
______ЃЛ
![]() ШЫЫЕМззщЕФгХауТЪИпгкввзщгХауТЪЃЌЫљвдМззщГЩМЈБШввзщГЩМЈКУЃЌЕЋвВгаШЫЫЕввзщГЩМЈБШМззщГЩМЈКУЃЌЧыФуИјГіСНЬѕжЇГжввзщГЩМЈКУЕФРэгЩЃЎ
ШЫЫЕМззщЕФгХауТЪИпгкввзщгХауТЪЃЌЫљвдМззщГЩМЈБШввзщГЩМЈКУЃЌЕЋвВгаШЫЫЕввзщГЩМЈБШМззщГЩМЈКУЃЌЧыФуИјГіСНЬѕжЇГжввзщГЩМЈКУЕФРэгЩЃЎ