题目内容
【题目】(1)阅读下面材料:
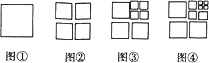
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .
【答案】(2)①3,3,4;②|x+1|,1或﹣3;③﹣1、0、1、2.
【解析】
根据两点之间的距离是哪些线段的和差以及绝对值的性质即可得到两点之间的距离公式,根据到两点的距离之和最小时这个点应该在已知的两点所确定的线段上
解:(2)①5-2=3,-2-(-5)=3,1-(-3)=4
②数轴上表示x和﹣1的两点A和B之间的距离是![]()
∵|x+1|=2,
∴x+1=±2,
∴x=1或﹣3,
(3)由题意可知:|x+1|+|x﹣2|表示数x到﹣1和2之间的距离之和,
∴当﹣1≤x≤2时,
|x+1|+|x﹣2|可取得最小值,
∴x的整数为﹣1,0,1,2;
故答案为:
(1)3;3;4
(2)|x+1|;1或﹣3
(3)﹣1,0,1,2

练习册系列答案
相关题目