Question

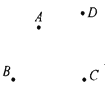
【题目】如图，豫东有四个村庄A、B、C、D．现在要建造一个水塔P．请回答水塔P应建在何位置，才能使它到4村的距离之和最小，说明最节约材料的办法和理由．

Answer 1

【答案】说明见解析.

【解析】试题分析：根据线段的性质：两点之间，线段距离最短；结合题意，要使它与四个村庄的距离之和最小，就要使它在AC与BD的交点处．

试题解析：

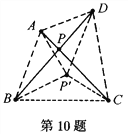
如图，水塔P应建在线段AC和线段BD的交点P处。这样的设计将最节省材料.

理由：我们不妨任意取一点P′,连接AP′、BP、CP′、DP′、AB、BC、CD、DA，

∵△AP′C中,AP′+CP′>AC=AP+CP，①

在△BP′D中,BP′+DP′>BD=BP+DP，②

①+②得AP′+BP′+CP′+DP′>AP+BP+CP+DP.

∵点P′是任意的，代表一般性，

∴线段AC和BD的交点处P到4个村的距离之和最小.