题目内容
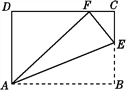
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,ACB的顶点A在△ECD的斜边DE上 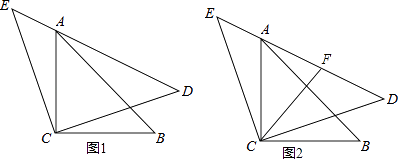
(1)求证:AE2+AD2=2AC2;
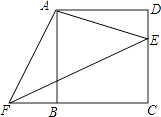
(2)如图2,若AE=2,AC=2 ![]() ,点F是AD的中点,直接写出CF的长是 .
,点F是AD的中点,直接写出CF的长是 .
【答案】
(1)证明:连结BD,如图所示:

∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.
∵∠ECD﹣ACD=∠ACB﹣∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,  ,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC=45°,CE=CD,
∴∠BDA=∠BDC+∠ADC=90°,
在Rt△ADB中.∵AD2+BD2=AB2,
∴AD2+AE2=2AC2.
(2)2 ![]()
【解析】(2)解:由(1)得:CE=CD,AE2+AD2=2AC2; ∴∠E=∠CDA,22+AD2=2×(2 ![]() )2 ,
)2 ,
解得:AD=4,
∵点F是AD的中点,
∴AF=DF=2=AE,
∴EF=DA,
在△CEF和△CDA中,  ,
,
∴△CEF≌△CDA(SAS),
∴CF=CA=2 ![]() ;
;
所以答案是:2 ![]() .
.
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目