题目内容
【题目】(14分)定义:底与腰的比是![]() 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
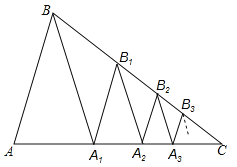
如图,已知△ABC中,AB=BC,∠C=36°,BA1平分∠ABC交AC于A1.

(1)![]() =AA1A C;
=AA1A C;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An.(n为大于1的整数,直接回答,不必说明理由)
【答案】(1)证明见试题解析;(2)△ABC是黄金等腰三角形;(3)![]() .
.
【解析】
试题分析:(1)由角平分线的性质和相似三角形的判定与性质,得到△ABC∽△AA1B,从而有![]() ,求出即可;
,求出即可;
(2)设AC=1,则AB2=1﹣AB,求出AB的值,进而得出![]() =
=![]() ,即可得出结论;
,即可得出结论;
(3)利用(2)中所求进而得出AA1,A1A2的长,进而得出其长度变化规律求出即可.
试题解析:(1)∵AC=BC,∠C=36°,∴∠A=∠ABC=72°,∵BA1平分∠ABC,∴∠ABA1=![]() ∠ABC=36°,∴∠C=∠ABA1,又∵∠A=∠A,∴△ABC∽△AA1B,∴
∠ABC=36°,∴∠C=∠ABA1,又∵∠A=∠A,∴△ABC∽△AA1B,∴![]() ,即
,即![]() =AA1A C;
=AA1A C;
(2)△ABC是黄金等腰三角形,理由:
由(1)知,![]() =AA1A C,设AC=1,∴
=AA1A C,设AC=1,∴![]() =AA1,又由(1)可得:AB=A1B,∵∠A1BC=∠C=36°,∴A1B=A1C,∴AB=A1C,∴AA1=AC﹣A1C=AC﹣AB=1﹣AB,∴
=AA1,又由(1)可得:AB=A1B,∵∠A1BC=∠C=36°,∴A1B=A1C,∴AB=A1C,∴AA1=AC﹣A1C=AC﹣AB=1﹣AB,∴![]() =1﹣AB,设AB=x,即
=1﹣AB,设AB=x,即![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() (不合题意舍去),∴AB=
(不合题意舍去),∴AB=![]() ,又∵AC=1,∴
,又∵AC=1,∴![]() =
=![]() ,∴△ABC是黄金等腰三角形;
,∴△ABC是黄金等腰三角形;
(3)由(2)得;当AC=a,则AA1=AC﹣A1C=AC﹣AB=a﹣AB=![]() =
=![]() ,
,
同理可得:A1A2=A1C﹣A1B1=AC﹣AA1﹣A1B1
=![]() =
=![]() =
=![]() ;
;
故An﹣1An=![]() .
.

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案