Question

如图，在△ABC和△DBC中，已知∠ACB=∠DBC=90°，点E为BC的中点，DE⊥AB，垂足为F，且AB=DE．
（1）求证：△DBC是等腰Rt△；
（2）若BD=8cm，求AC的长；
（3）在（2）的条件下求BF的长．

Answer 1

分析：（1）根据三角形的内角和定理求出∠1=∠3，根据AAS推出△ACB≌△EBD，推出BC=BD即可；
（2）根据全等得出AC=BE，求出BE的长即可；
（3）根据勾股定理求出DE，根据三角形的面积公式即可求出BF．

解答：（1）证明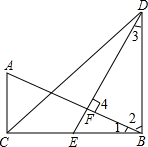：∵DE⊥AB，
∴∠4=90°=∠ACB=∠EBD，
∴∠1+∠2=90°，∠2+∠3=90°，
∴∠1=∠3，
在△ACB和△EBD中，
∵

∠1=∠3 ∠ACB=∠EBD AB=DE

，
∴△ACB≌△EBD（AAS），
∴BC=BD，
∵∠EBD=90°，
∴△CBD是等腰直角三角形；

（2）解：∵BC=BD=8cm，△ACB≌△EBD，
∴AC=BE，
∵E为BC中点，
∴BE=

1

2

BC=4cm，
∴AC=BE=4cm；

（3）解：在Rt△EBD中，BD=8cm，BE=4cm，由勾股定理得：DE=4

5

cm，
在△EBD中，S_△EBD=

1

2

×BE×BD=

1

2

×DE×BF，
∴BE×BD=DE×BF，
∴4cm×8cm=4

5

cm×BF，
∴BF=

8 5

5

cm．

点评：本题考查了全等三角形的性质和判定，三角形的内角和定理，等腰直角三角形性质，勾股定理等知识点的综合运用，通过做此题培养了学生的分析问题和解决问题的能力．