题目内容
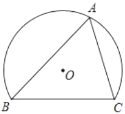
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() 是弧
是弧![]() 的中点,弦
的中点,弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
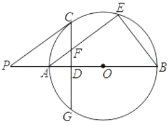
【答案】(1)详见解析;(2)![]() .
.
【解析】
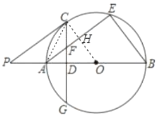
(1)连接OC,如图,先利用切线的性质得OC⊥PC,再利用垂径定理得到OC⊥AE,所以PC∥AE;
(2)设OC与AE交于点H,如图,利用垂径定理得到![]() ,根据圆周角定理得
,根据圆周角定理得![]() ,则AF=CF=5,在
,则AF=CF=5,在![]() 中利用三角函数的定义可计算出
中利用三角函数的定义可计算出![]() ,
,![]() ,进而证明
,进而证明![]() ,得到AH=CD=8,所以AE=2AH=16,然后证明
,得到AH=CD=8,所以AE=2AH=16,然后证明![]() ,于是利用相似比可计算出BE.
,于是利用相似比可计算出BE.
证明:(1)连接![]() ,如图,
,如图,
∵![]() 为
为![]() 的切线,
的切线,
∴![]() ,
,
∵![]() 是弧
是弧![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ;
;
(2)设![]() 与
与![]() 交于点
交于点![]() ,如图,
,如图,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中
中
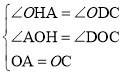 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
故答案为:12.

练习册系列答案
相关题目